错题

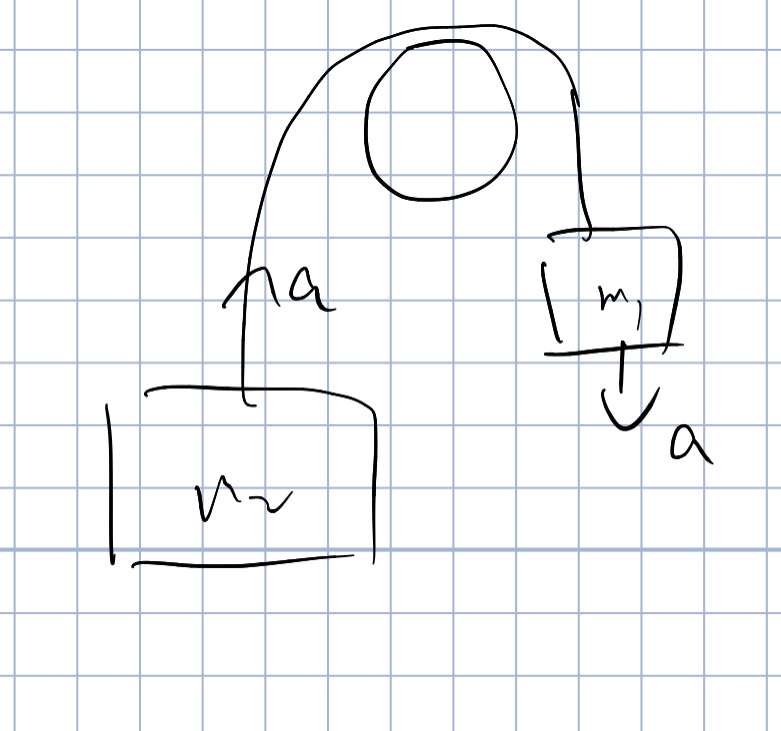
单摆

对于一个摆长不变的摆，我们有T=2πlgT=2\pi\sqrt{\frac{l}{g}}

若底下有木板铺满细沙经过，则有图像

png

png

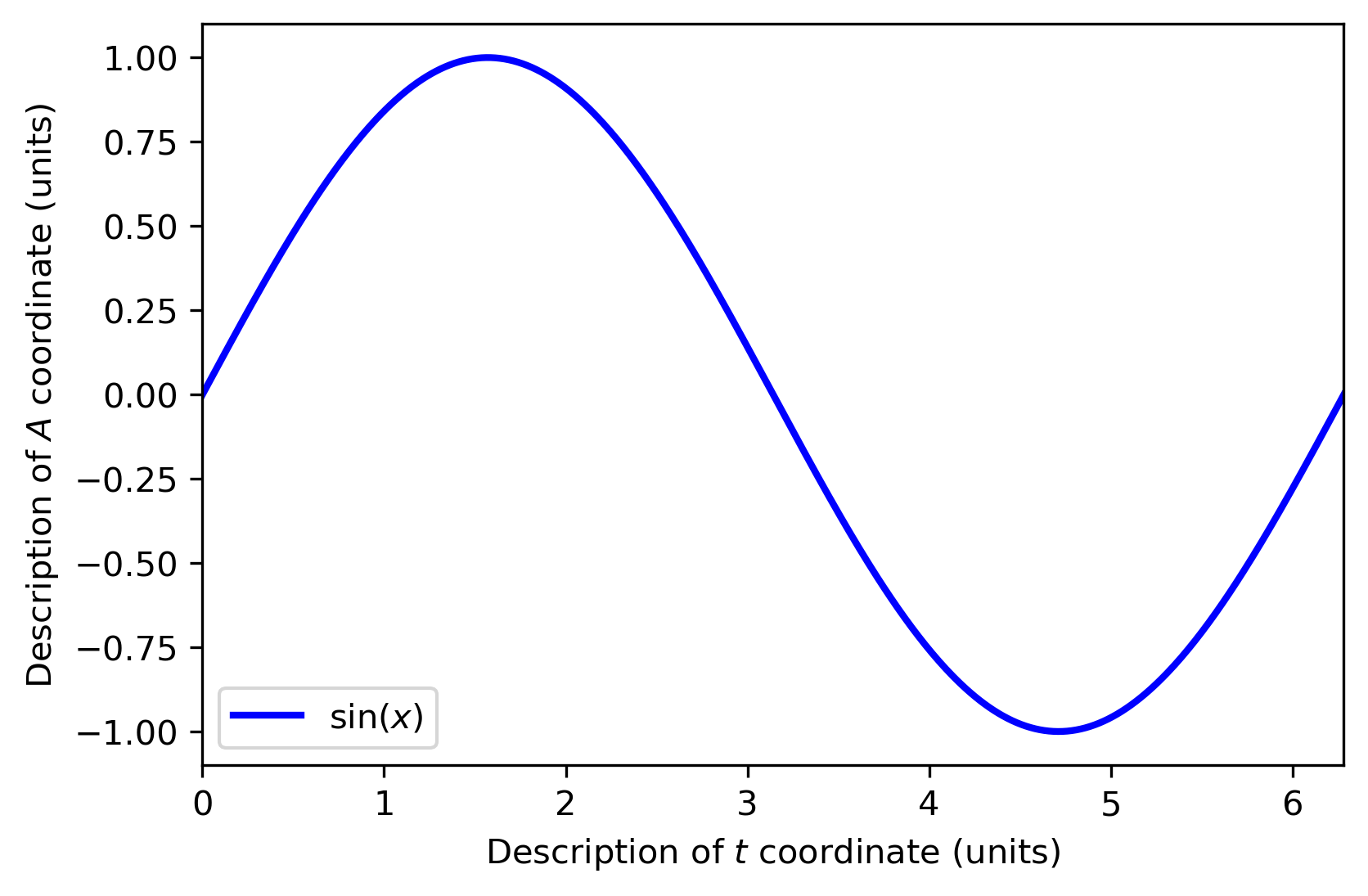
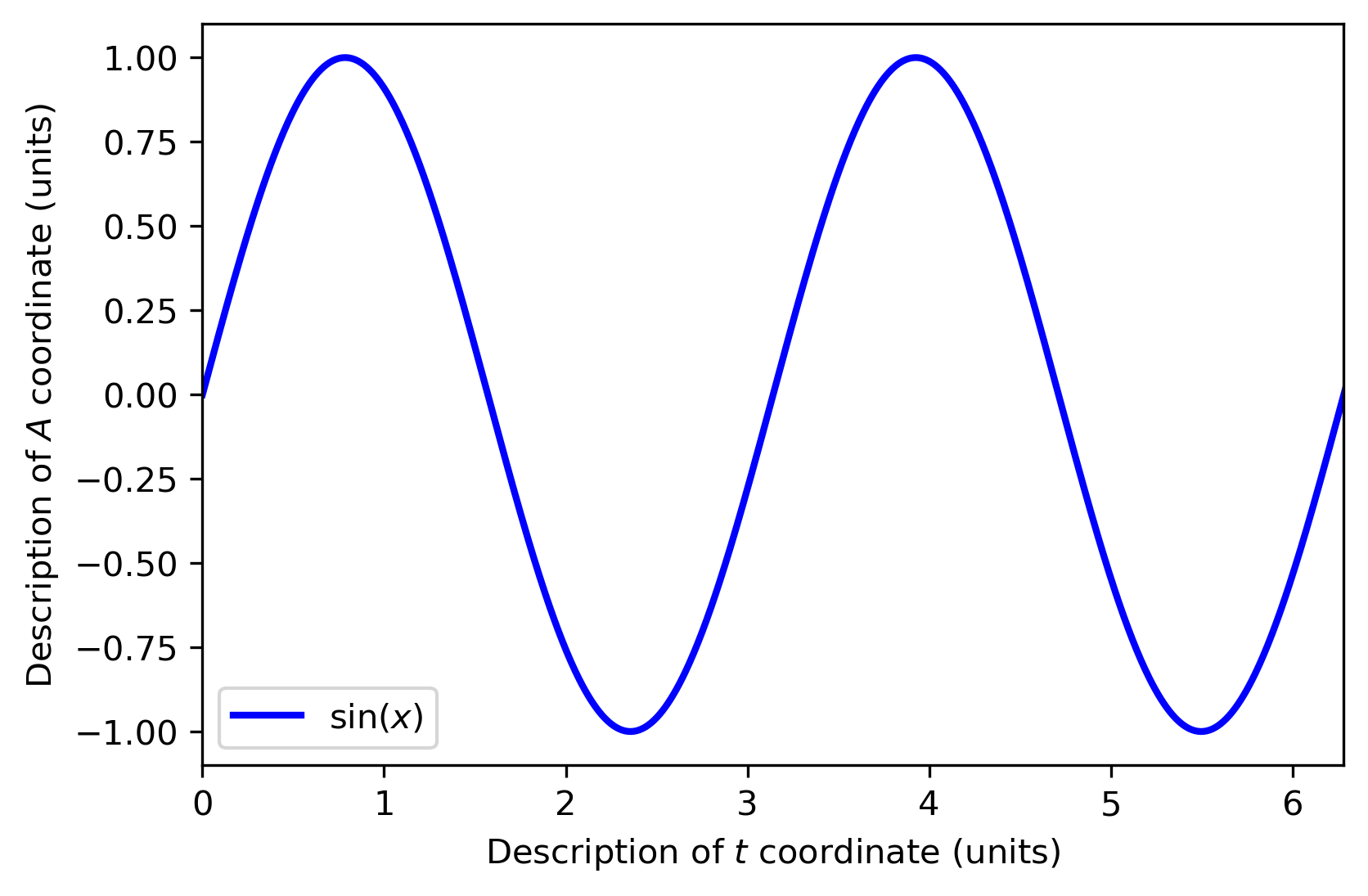
可以看出图一中单摆只走了一个周期，而图二中有两个周期

意味着图一的木板抽出的时间是一个周期，而图二是两个

故图一的木板更快

动量守恒定律

2.png

m1v1⃗+m2v2⃗=m1v1′⃗+m2v2′⃗m_1\vec{v_1}+m_2\vec{v_2}=m_1\vec{v_1'}+m_2\vec{v_2'}

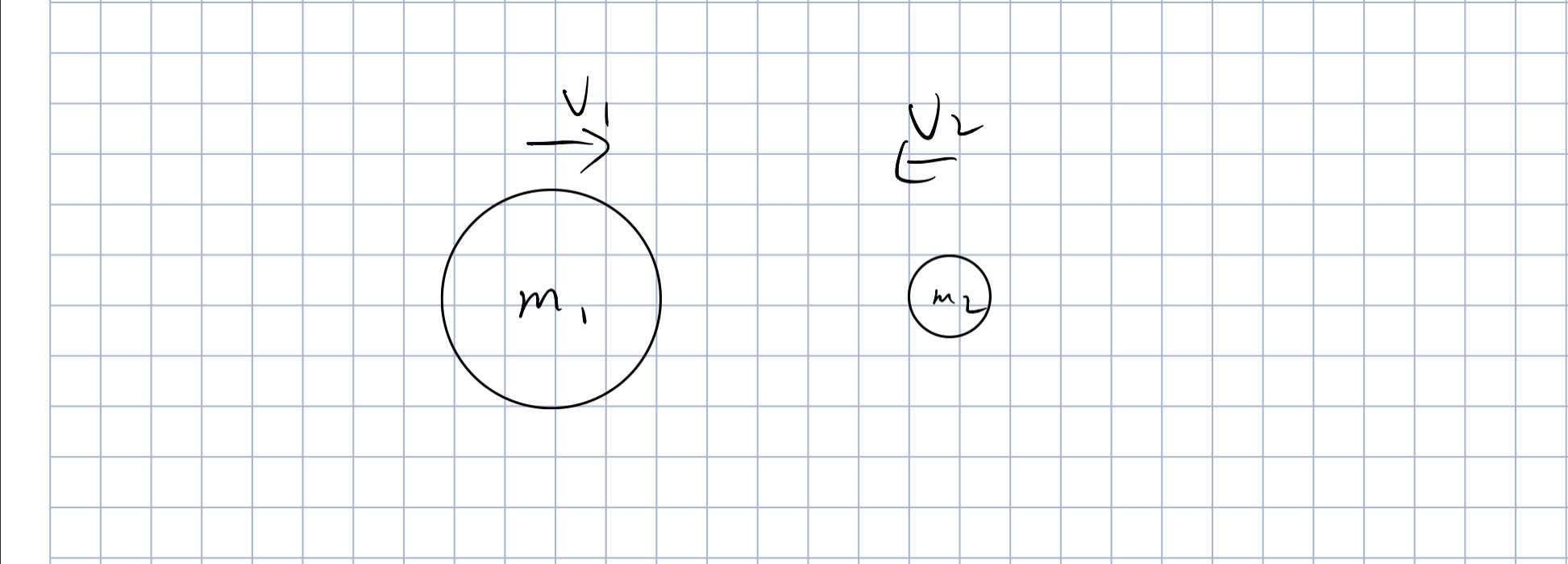
这提示你，动量的改变量是个矢量，速度从-2到正2是需要冲量帮忙改变的。做的是4m的活

小结论

1.png

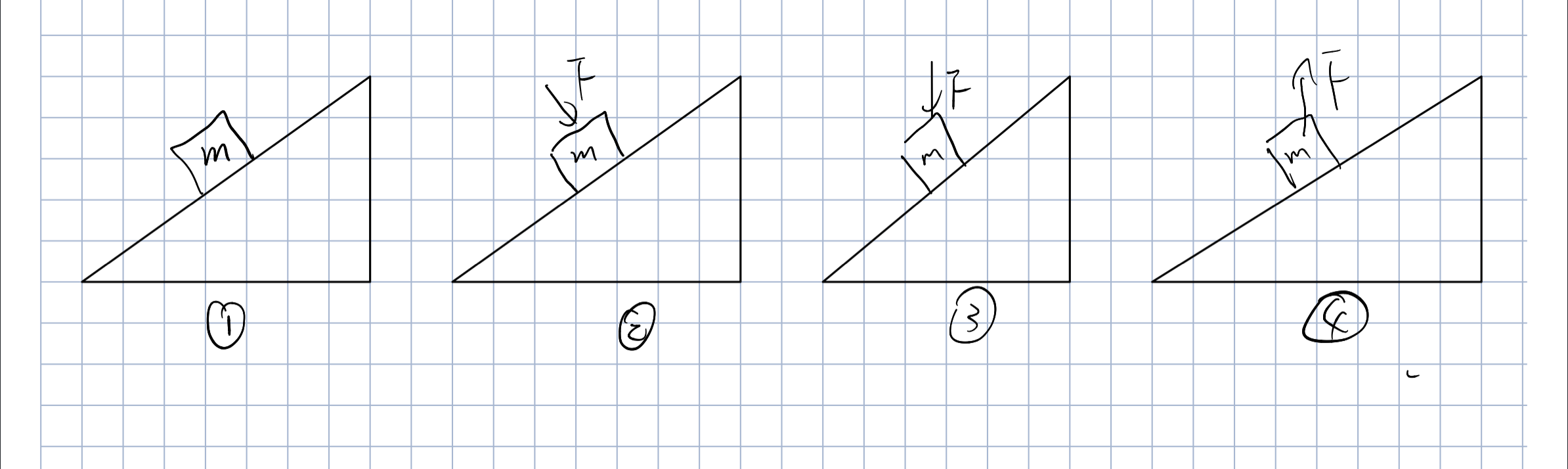
斜面均有摩擦力且物块均会下滑，且斜面不动

第一种情况

无论m多大，加速度都不变，为a=gsinθ−μgcosθa = gsin\theta -\mu gcos\theta

其中gsinθgsin\theta是重力加速度在该方向的分量

μgcosθ\mu gcos\theta则是求出来的

第二种情况

合理推广，受到的摩擦力更大了，因此a减小

第三，四种情况

相当于一个物块重力改变了，但是质量却没有变，套用第一种情况得知

向下时加速度增大，向上时加速度减小

消去

圆锥摆

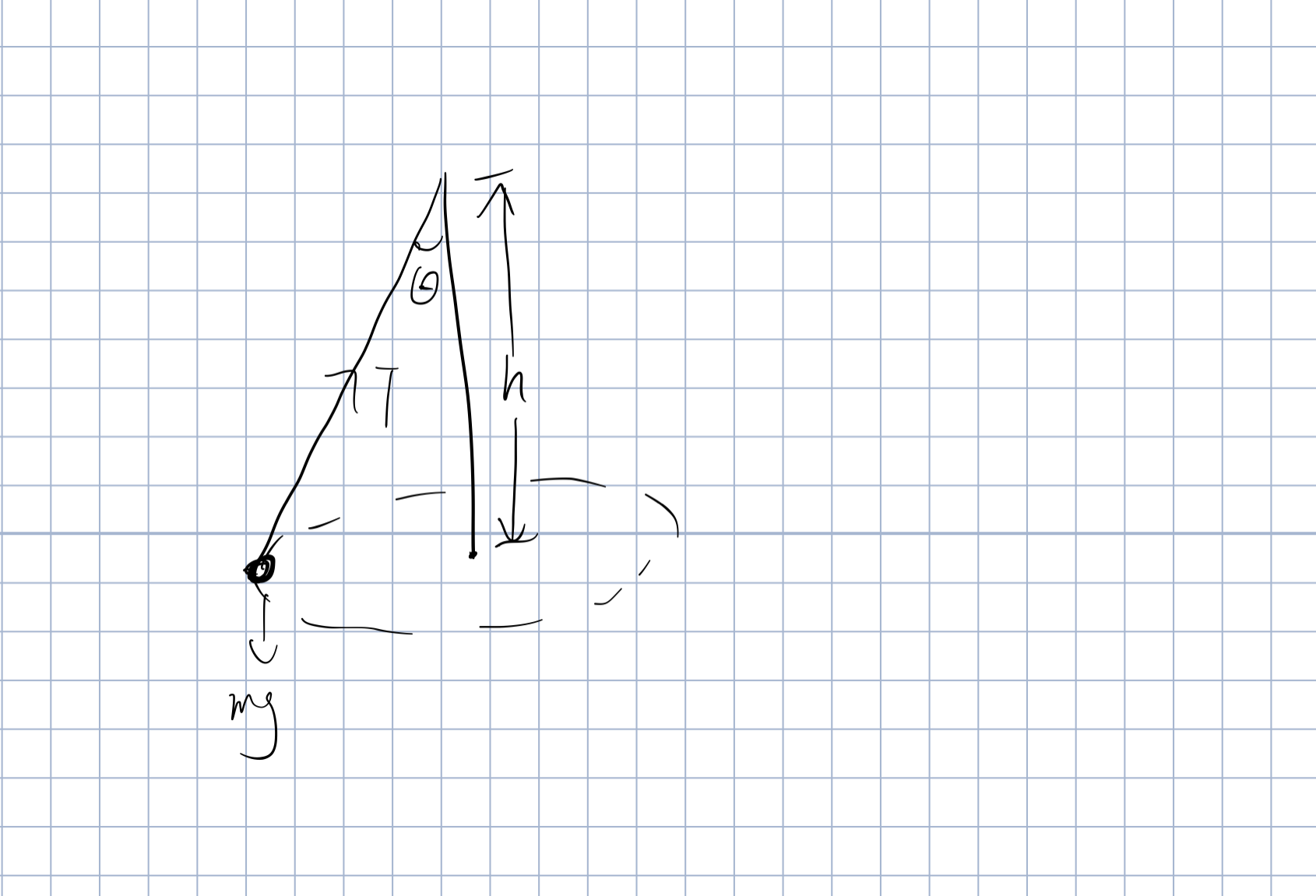
10.png

有向心力F=mgtanθ=mω2htanθ=m(2πT)2htanθF=mgtan\theta=m\omega^2htan\theta=m(\frac{2\pi}{T})^2htan\theta

有周期T=2πhgT=2\pi \sqrt{\frac{h}{g}}

只与高h有关

摩擦力做功

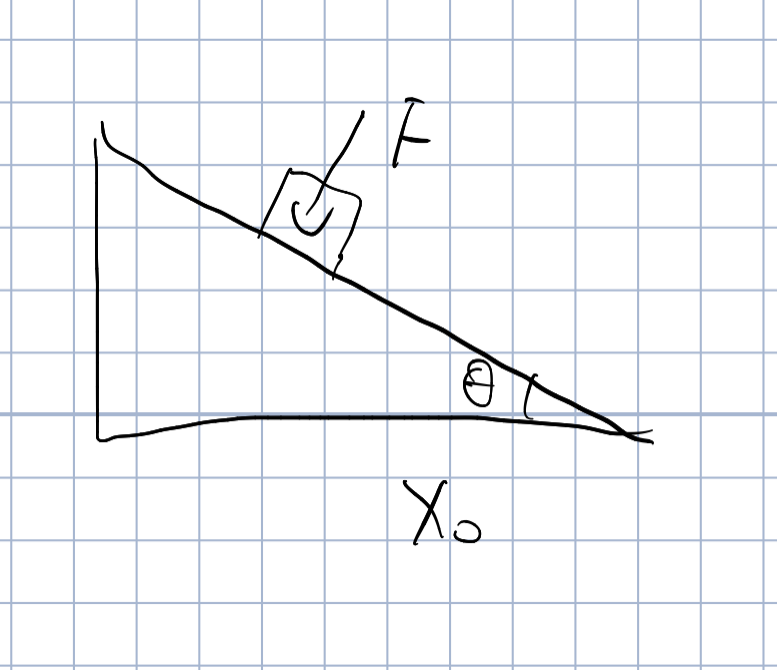
11.png

物块受到垂直斜面的力F，从顶部下落到底部

有摩擦力f=μ(mgcosθ+F)f=\mu (mgcos\theta+F)

做功W=f⋅x=fx0cosθ=(μmg+Fcosθ)x0W=f\cdot x=f\frac{x_0}{cos\theta}=(\mu mg+\frac{F}{cos\theta})x_0

有结论，当F为0时，摩擦力做功只与横坐标的路程有关，与角度无关

题目中的流体力学

白努力方程的简单推导

首先，需要满足，定常流，流体不可压缩，没有摩擦，流体按流线运动

定常流就是指一定时间里，通过的流体体积，密度是定值

比如这里5秒钟的流量是1L，明天来看还是5秒1L，这就是定常流

值得注意的是，我们可以对定常流进行研究，而不是我们制造定常流

因此定常流常出现在自然界，比如空气，水流，等等

伯努利方程实质上是流体的能量守恒

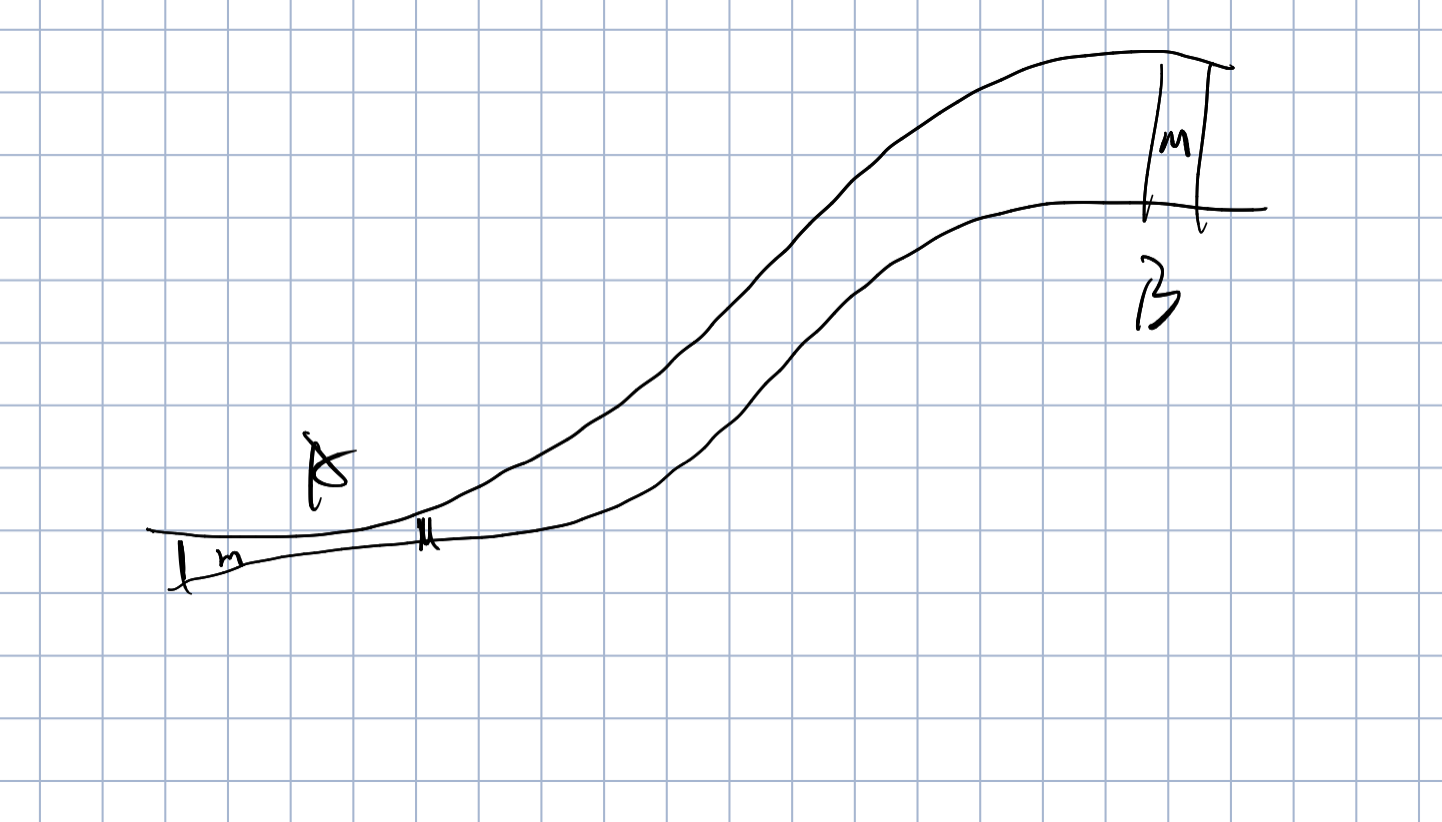
19.png

A点右侧受压强p1p_1，B点左侧受压强p2p_2

在ΔT\Delta T时间内左侧做功p1ΔVp_1\Delta V,右侧做功−p2ΔV-p_2\Delta V

有12mv12+mgh1+p1ΔV−p2ΔV=12mv22+mgh2\frac{1}{2}mv_1^2+mgh_1+p_1\Delta V-p_2\Delta V=\frac{1}{2}mv_2^2+mgh_2

也就是12mv2+mgh+pΔV=C\frac{1}{2}mv^2+mgh+p\Delta V=C

在这里引入压力势能的概念Ep=pΔVE_p=p\Delta V

如何理解压力势能，可以想象这里有一个膜，这段流体一流过去

这膜就对流体做负功，换言之，在没有流过去之前

这段体积的流体本来有这么多能量，一流过这膜，能量就用掉了

定常流

水流是典型的定常流。对于一个自由落体的水柱来说

Δt\Delta t时间内流过一个横截面的V一样，但是底下越流越快

所以越来越窄

如果是一个米粒定常流的话，就是一定时间内流过一个横截面的米粒数一样

如果利用定常流这一条件呢

不妨我们把视角放在流体的源头，或者叫流体的源（与“汇”相对偶的概念）

我们知道，在任意相同的Δt\Delta t时间内，流出的ΔM\Delta M一定相同

则记ΔMΔt=M0\frac{\Delta M}{\Delta t}=M_0其中M0M_0为常数

由于任意Δt\Delta t，所以当Δt⟶dt\Delta t \longrightarrow dt时，仍成立

即dMdt=M0\frac{dM}{dt}=M_0所以有dM=M0dtM=M0t+C\begin{array}{l}dM=M_0dt\\M=M_0t+C\end{array}

物理意义在于流体的源的发出量与时间是一个一次函数关系

流体的重力势能

这里以米粒定常流为例

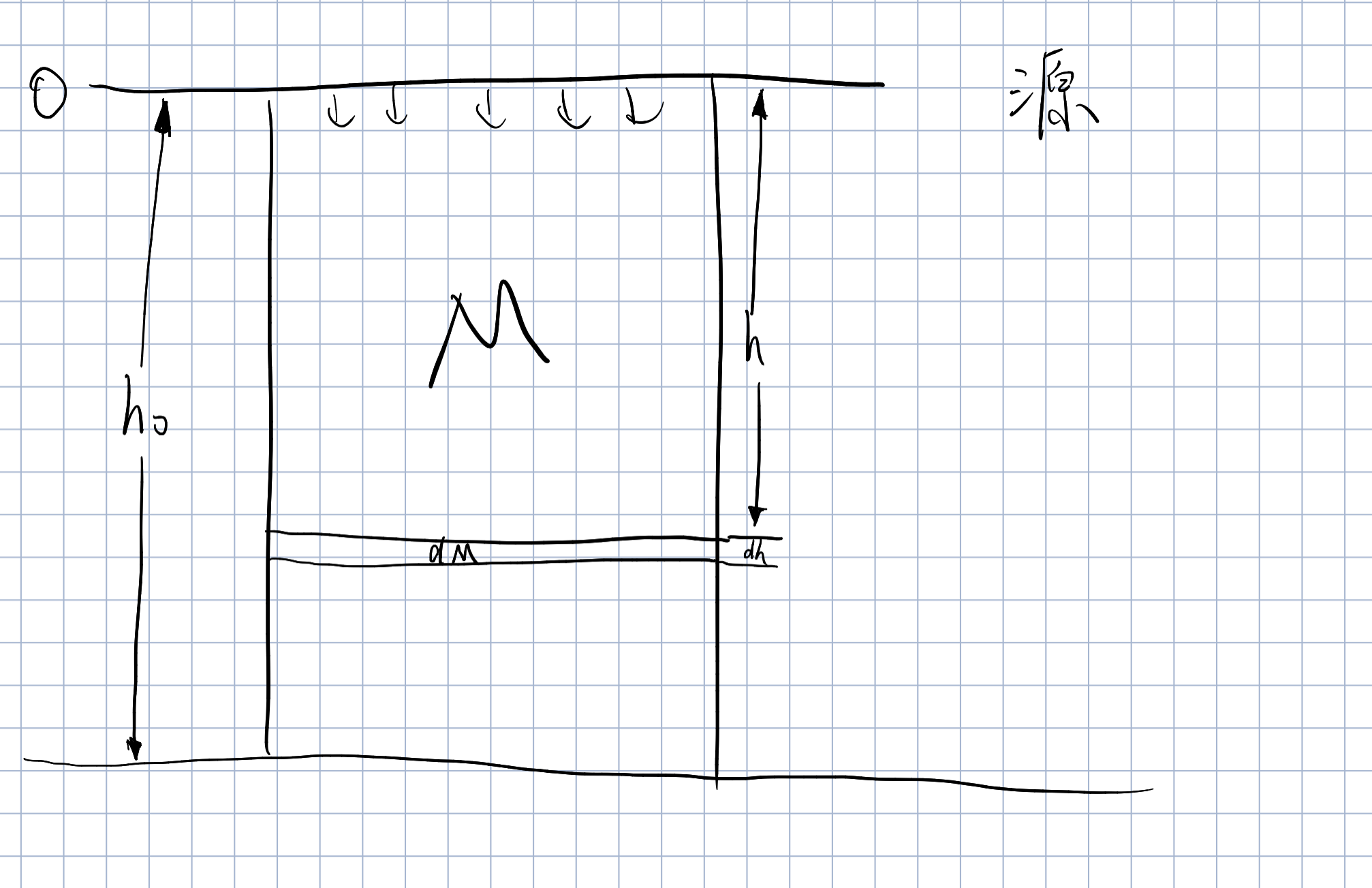
20.png

为方便讨论，以上界为零势面，之后所有算的重力势能先不加负号，算完了一起加

以及，上界为流体源，流体初速度为零，忽略空气阻力

由定常流，有结论dM=M0dtM=M0t\begin{array}{l}dM=M_0dt\\M=M_0t\end{array}

整体思路是，求出每一个dMdM的重力势能，再把它们按照高度都累积起来

对于任意一个dMdM来说，其重力势能dEp=ghdMdE_p = ghdM

可是M和h有什么关系呢？我们发现，dMdM落到h处的时间t可求

由于米粒做自由落体运动，所以时间t有h=12gt2t=2hg\begin{array}{l}h=\frac{1}{2}gt^2\\t=\sqrt{\frac{2h}{g}}\end{array}

而时间t和M又是有确切关系的，所以dhdt=gt=2ghdt=dh2gh\begin{array}{l}\frac{dh}{dt}=gt=\sqrt{2gh}\\dt=\frac{dh}{\sqrt{2gh}}\end{array}

dM=M0dt=M0⋅12ghdhdM=M_0dt=M_0\cdot \frac{1}{\sqrt{2gh}}dh

所以dEp=ghdM=M0g2h12dhdE_p=ghdM=M_0\sqrt{\frac{g}{2}}h^{\frac{1}{2}}dh

则Ep=∫0h0M0g2h12dh=M0⋅23g2h0h0E_p=\int_0^{h_0}M_0\sqrt{\frac{g}{2}}h^{\frac{1}{2}}dh=M_0\cdot \frac{2}{3}\sqrt{\frac{g}{2}}\sqrt{h_0}h_0

其中h0=g2t0M0t0=Mtotal\begin{array}{l}\sqrt{h_0}=\sqrt{\frac{g}{2}}t_0\\M_0t_0=M_{total}\end{array}

t0t_0意思是在这个时间下落到h0h_0

结论

Ep=13Mtotalgh0E_p=\frac{1}{3}M_{total}gh_0

最后再加个 负号

回顾

回顾整个推导过程，其实我们会发现，还有另一种理解

就是把整个系统当作一个密度不均匀的物体，由于定常流所以这个物体基本上可以算不动

然后我们的操作就是按照它的质量分布进行加权平均而已

简单电路

3.png

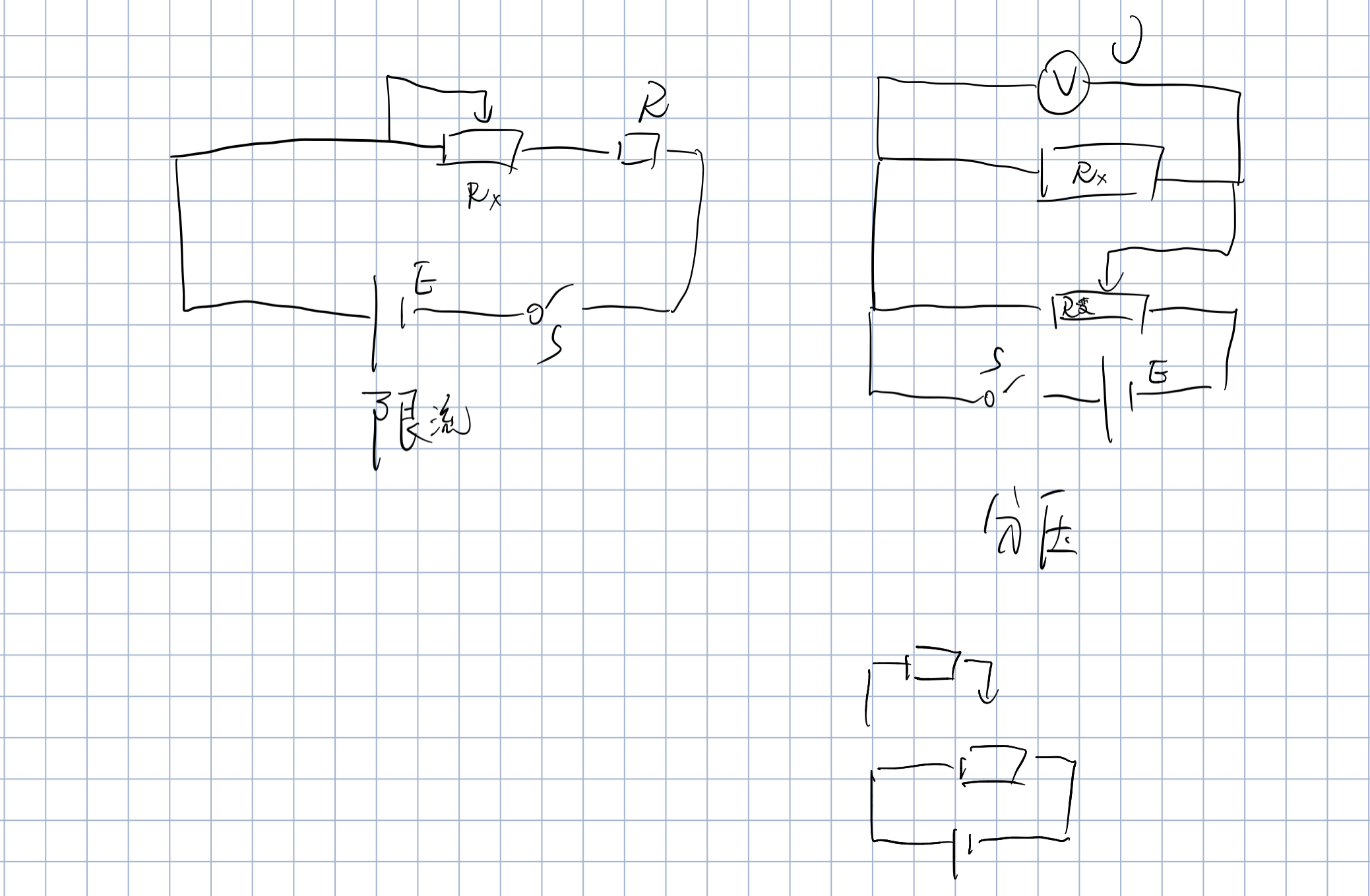
限流电路

可控范围有限，拥有烧表风险

在待测电阻过大时，调节滑动变阻器改变的电压太小

换更大阻值的滑变有可能导致电流太小无法测出，比较麻烦

在待测电阻较小时，适合使用限流接法，同时滑变阻值应稍大

但是待测较小时可能电流太大，烧表。

分压电路

本质上是待测电阻直接接在了一个闭合回路上，使得针头分的压就是我的电压

显然该电路电压可以从零开始

烧表风险较小，因为你可以一直看着电流表，如果电流表快到最大示数，停下即可

适用于各种场景，几乎没有限制

天体

4.png

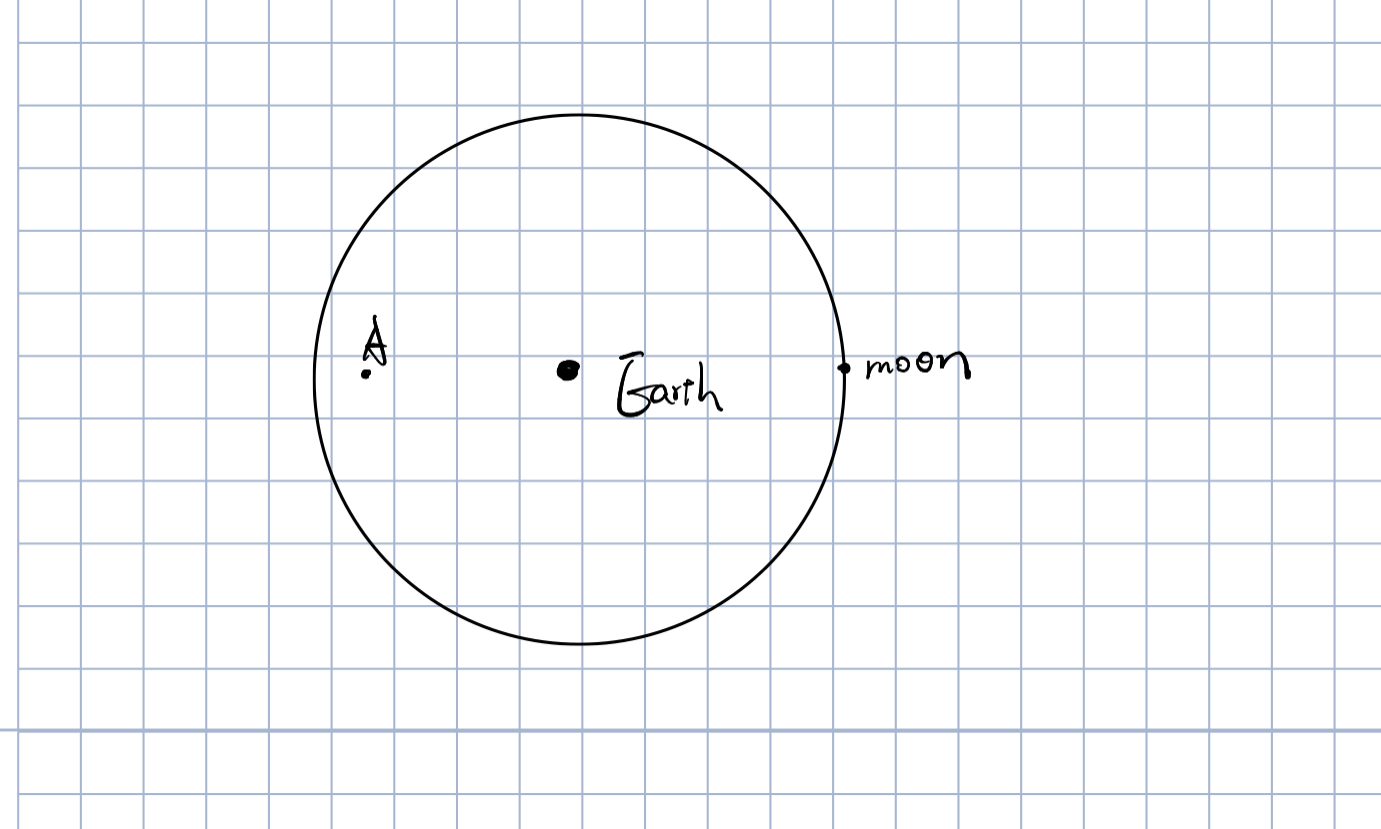
试问图中A点是否可能是拉格朗日点

分析拉格朗日点的特点

受到地球和月球的两个力，并平衡在那里

推知，角速度必与月球相同。

根据角速度的公式有ω=GMR3\omega = \frac{GM}{R^3}

知道同一个中心天体的同一轨道上的物体的角速度相同

这意味着，在月球轨道上卫星本可以与月球有相同的角速度

现在因为多受到月球的引力而需要更大的角速度来用掉多余的力

自然A点需要更大的角速度，也就没法是拉格朗日点了

能量

问做功需要写清正负，至于怎么判断做功，其实很简单

E0+Wf=E0′E_0+W_f=E_0'

这个式子是说，初状态的能量加别的力做的功等于末状态的能量

注意什么叫别的力，比如在重力场中，若选择E为机械能，那么重力就不能叫别的力，因为机械能守恒

但是摩擦力就是别的力

同理在电场中也是一个道理，但在电场中我们通常把动能和电势能分开来看

其实在重力场中我们也分开来看就好了，不麻烦

对于任意势能

有E0−Wf=E0′E_0-W_f=E_0'

等式的含义是，原有的势能减去该力对外做的功等于现在的势能

或者说，势能把一部分拿出去做功去了

或者写成Wf=−ΔEW_f=-\Delta E

能量守恒的本质

能量守恒最本质也是最朴素的想法就是一种形式的能转化为另一种形式的能

举例

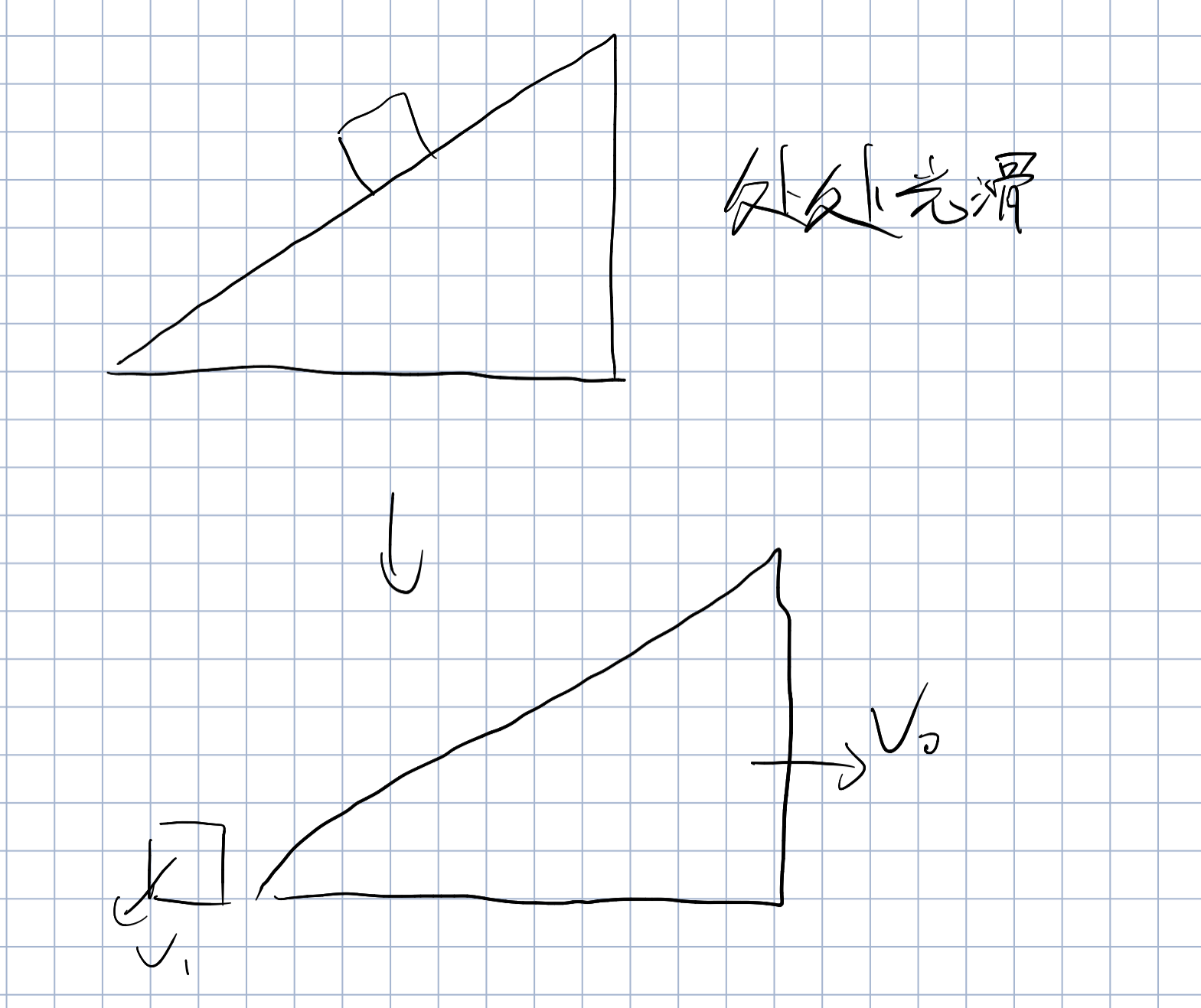
13.png

小物块的所有重力势能转化为了自己的动能和斜面的动能

如何理解此时斜面对小物块做负功呢。

换句话也可以说，小物块对斜面的压力做正功

小物块把自己的能量通过做正功的方式给了斜面

这里蕴涵了另一件深刻的道理，你对别人做正功

别人的能量理应增加，你的能量理应减少

根据牛顿第三定律，别人对你的反作用力对你做负功

推广

首先在宇宙中选定一个绝对静止的参考系，因为在不同参考系里做功大小不同

一个超人在空中以初速度v0v_0飞了起来，做抛体运动，到最高点的过程中

地球对超人的引力一直做负功，换言之，一直在阻碍超人运动

但相反的是，超人对地球的引力一直在做正功，因为地球相对绝对静止参考系运动了

这就是超人把自己的能量通过做正功的方式传递给了地球

但是注意到，这里并没有完全传递，还有一部分能量被暂存了起来，成为了重力势能

超人下落的过程中，这一部分势能被完全释放，变为地球和超人的动能

结论

当研究一个物体对另一个物体做了负功的时候

另一个物体既可以立即利用反作用力施加正功，也可以把这部分本该施加的转化为势能，稍后释放

重力势能

势能的好处就在于只要看初末状态而不用分析过程

所以要看一个东西的重力势能变化，只需要看初末势能即可

14.png

如果你把一个吊在天花板的有质量的不可拉伸的绳弄直了

你的力看起来是向下的，但这个力却被绳子像定滑轮一样转向了

因此重力势能提高了

总的来说就是外力做功一定对系统的能量有改变

能量损失

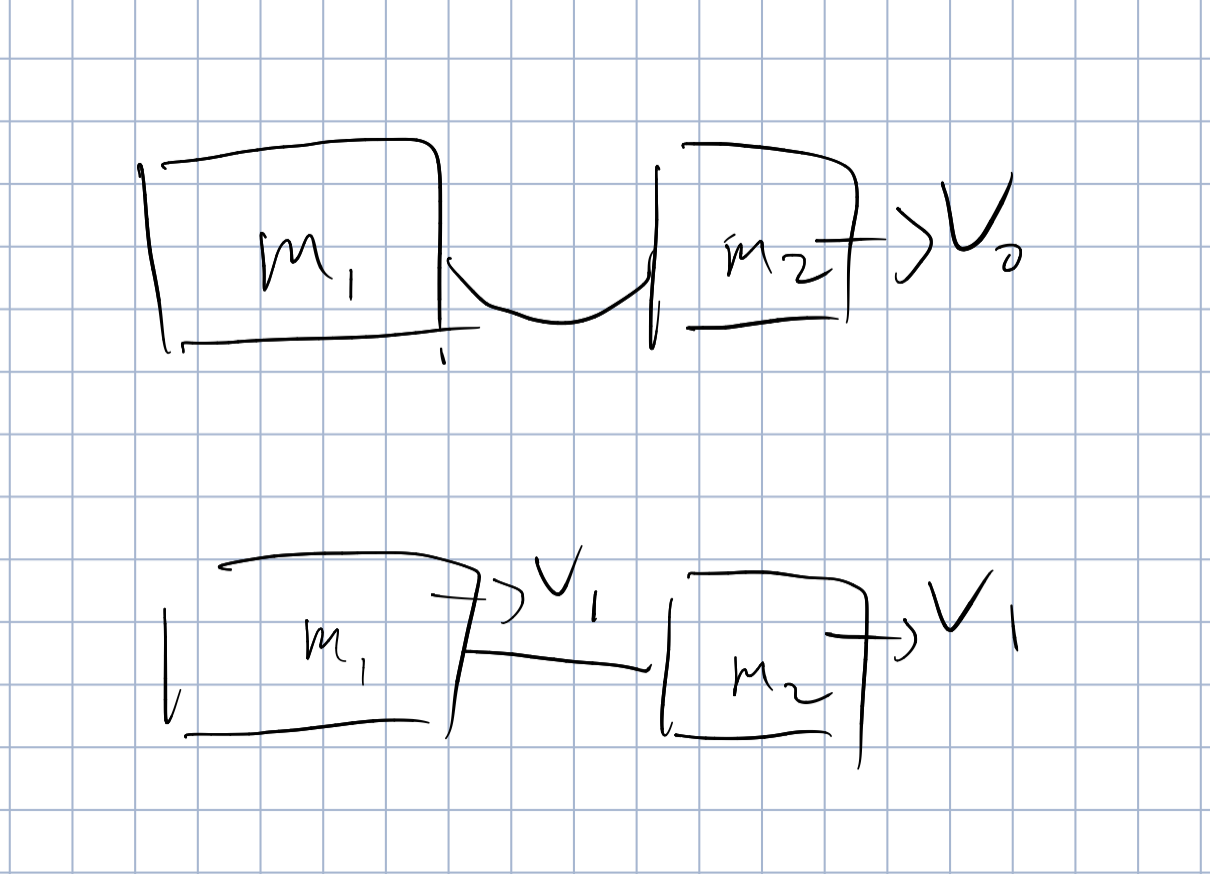
17.png

一开始m1m_1静止，m2m_2以v0v_0启动

之后共速，期间由动量守恒0+m2v0⃗=(m1+m2)v1⃗v1⃗=m2m1+m2v0⃗\begin{array}{l} 0+m_2\vec{v_0}=(m_1+m_2)\vec{v_1}\\ \vec{v_1}=\frac{m_2}{m_1+m_2}\vec{v_0} \end{array}

则ΔE=12[(m1+m2)v12−m2v02]=12m2v02(m2m1+m2−1)<0\Delta E = \frac{1}{2}[(m_1+m_2)v_1^2-m_2v_0^2]=\frac{1}{2}m_2v_0^2(\frac{m_2}{m_1+m_2}-1)<0

故有能量损失，损失在绳子的内能

还有一种情况，就是物块轰然坠地，此时物块的动能瞬间消失

做功的定义

力乘以该力施加的对象在力的方向上的位移

注意这个对象的位移需要满足两个条件，物体本身动了，力的接触点动了

举例来说，人的蹲起地面是不做功的

子弹射入木块，若是木块被固定住了，子弹也不对木块做功

因为功的全称，是机械功啊！

内能

通常我们说产生内能的时候，说一对摩擦力产生的内能，而不是一个摩擦力产生的内能

也就是说不能把两边产生的内能加起来，因为算f⋅xf\cdot x时就已经把所有产生的内能全算了

力学

受力平衡只针对静止或匀直物体而言，对于非静止或匀直物体，无受力平衡

受力平衡只针对静止或匀直物体而言，对于非静止或匀直物体，无受力平衡

受力平衡只针对静止或匀直物体而言，对于非静止或匀直物体，无受力平衡

简单来说就是一个物块静止时受力平衡，但是加速运动时，有一部分不能平衡，它们被用于提供加速度

5.png

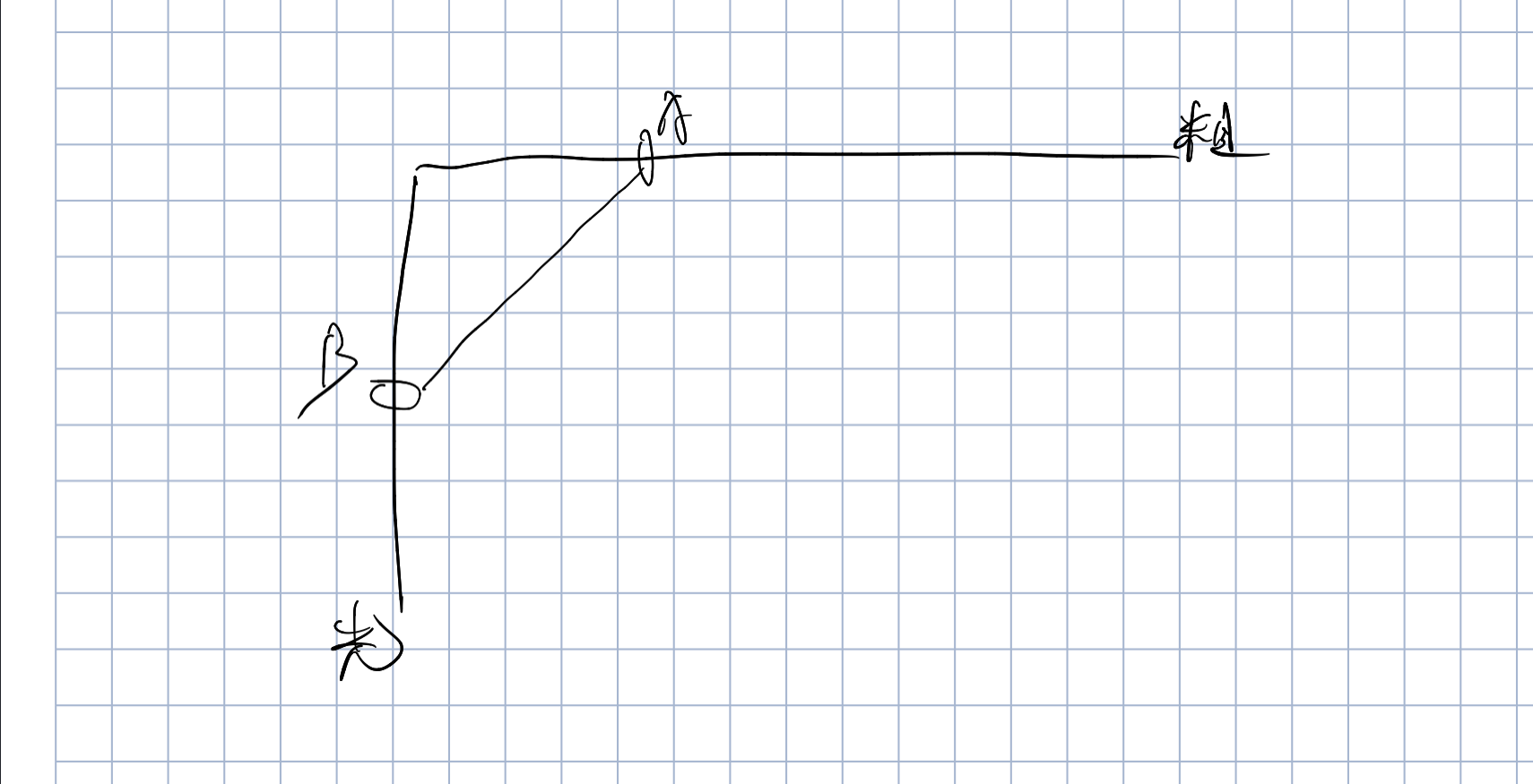
M不动，由于两物块有向下的加速度，故M所受支持力R<M+m1+m2R<M+m_1+m_2

再来一个

6.png

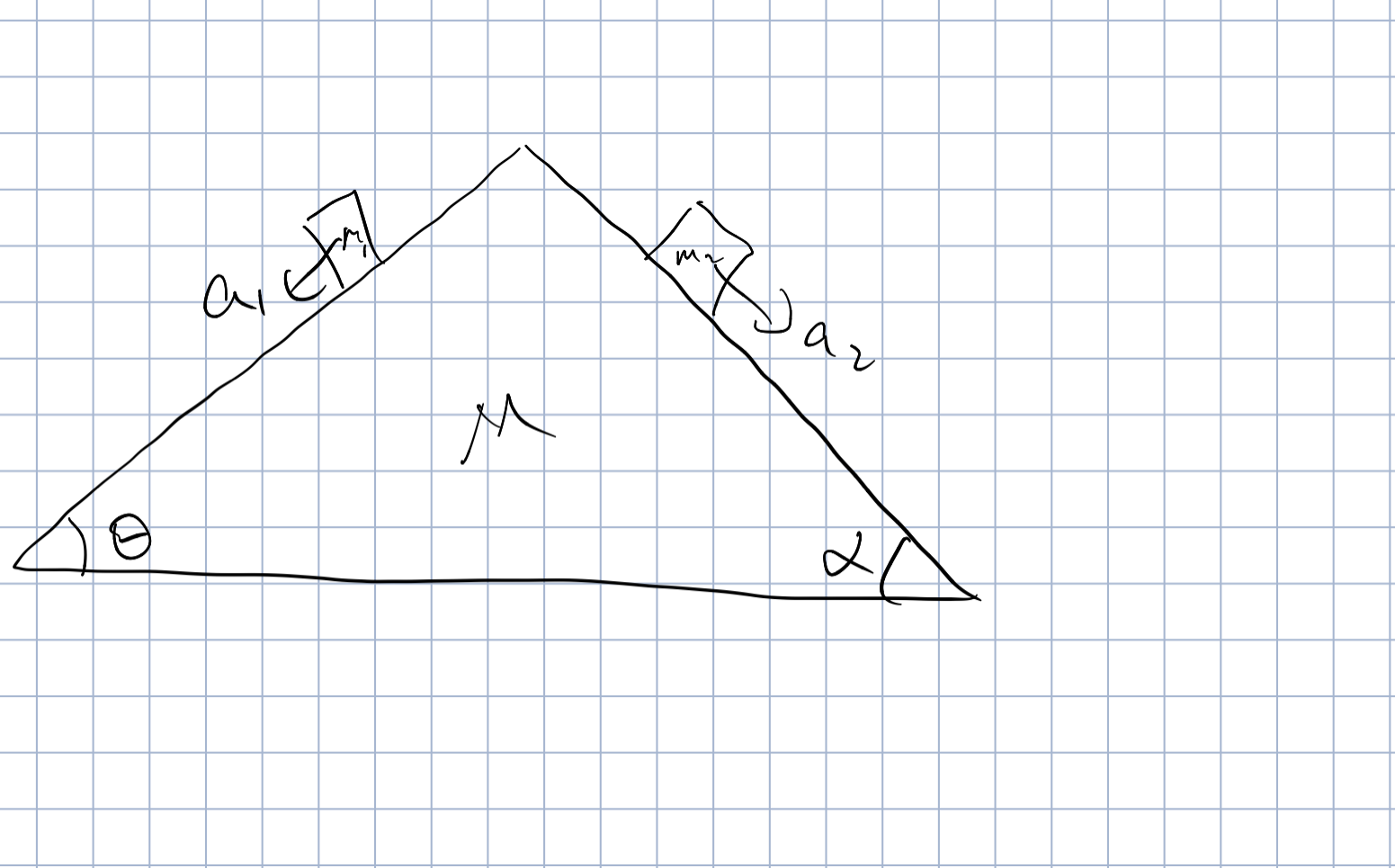
两种分析思路

一，B受到向下的重力和绳向上的拉力，这意味着B给绳向下的拉力一定等于自身重力

该拉力作用到A上，使得A看起来变成了A+B一样作用在杆上，所以上面的杆支持力为A+B

既然绳有向下的拉力则必有向左的拉力，B受到向右的拉力，那么B给绳向左的拉力与之相等

通过绳的传递，使得A受到向左的拉力，杆为了平衡，需要提供相应向右的摩擦力

这一摩擦力恰好与B所受杆向左的力相等，并且容易知道，绳子越平，这力就越大

二，整体考虑，杆给了所有的支持力，同时左右不动，意味着左右力相互抵消

力的叠加∑i=1nFi⃗=∑i=1nmia⃗i\sum_{i=1}^n\vec{F_i}=\sum_{i=1}^nm_i\vec a_i

平抛

7.png

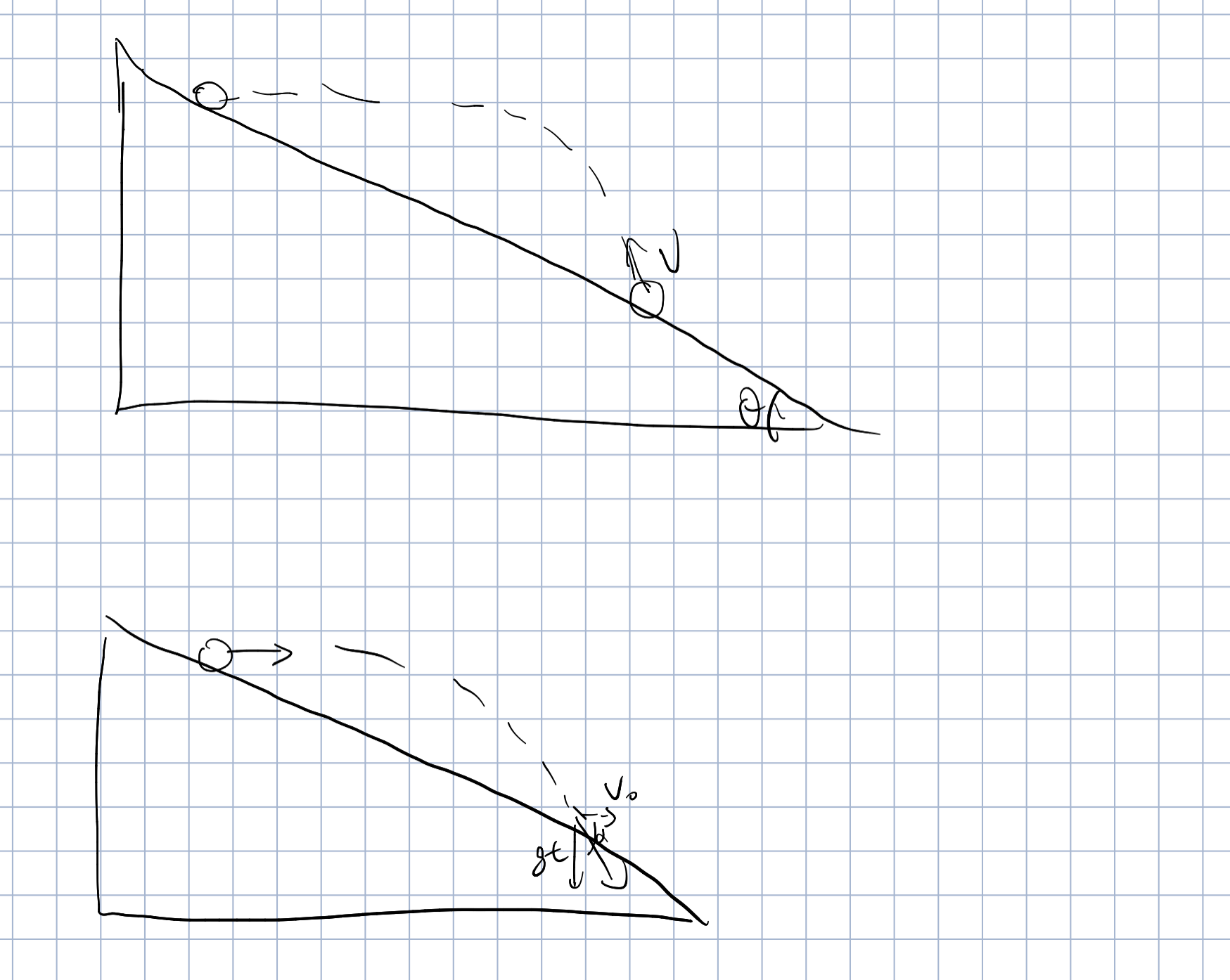
如果问向上抛感觉很难，可以考虑其 逆过程

对于斜面平抛来说必有tanθ=12gt2v0t=gt2v0tan\theta=\frac{\frac{1}{2}gt^2}{v_0t}=\frac{gt}{2v_0}

以及tanα=gtv0tan\alpha =\frac{gt}{v_0}

立刻有tanα=2tanθtan\alpha =2tan\theta

结论

对于斜面平抛而言，落地速度方向是一定的

那么同理，想要使上抛物体水平碰撞到斜面，则出手速度方向一定

又有推论一次完整的斜抛就是从顶点开始的两个平抛的组合，利用以上结论即可

绳子

绳子是一种神奇的东西，它所能施加的力一定沿着绳的方向

滑轮也是一种神奇的东西，它可以改变力的方向

将二者结合在一起，我们可以得到一个新的系统，这个系统以绳为方向

18.png

以绳为方向可以有另一种矢量m1g⃗−T⃗+T⃗−m2g⃗=m1g⃗−m2g⃗=(m1+m2)a⃗m_1\vec g -\vec T +\vec T-m_2\vec g=m_1\vec g -m_2\vec g=(m_1+m_2)\vec a

由于矢量的方向只有沿绳的正负，因此又可以把矢量符号去掉。直接算模长

矢量的分解

矢量的分解本质上是矢量合成的逆运算

由一个基本定理

若α1⃗,α2⃗,α3⃗...αn−1⃗,αm⃗\vec{\alpha_1},\vec{\alpha_2},\vec{\alpha_3}...\vec{\alpha_{n-1}},\vec{\alpha_m}

线性无关，且α1⃗,α2⃗...αn⃗,αn+1⃗\vec{\alpha_1},\vec{\alpha_2}...\vec{\alpha_{n}},\vec{\alpha_{n+1}}线性相关

则存在唯一的一组k1,k2...kn,kn+1k_1,k_2...k_n,k_{n+1}使得

k1α1⃗+k2α2⃗+...+knαn⃗+kn+1αn+1⃗=0k_1\vec{\alpha_1}+k_2\vec{\alpha_2}+...+k_n\vec{\alpha_n}+k_{n+1}\vec{\alpha_{n+1}}=0

说成人话就是一个n维向量可以被n个线性无关的基底唯一表示

关键是要看看我们想要分解的量是由什么合成的，再根据那个分解即可

对于一个斜抛的篮球，我们容易知道它的速度是由一个向下的加速度，和一个出手速度合成的

那我们就可以把篮球的速度分解为一个匀直斜向上，一个加速向下

易错点

做选择题时一定要注意物理量，把它们写出来，要不然容易错

比如∫Udt=R∫Idt=RQ\int Udt=R\int Idt=RQ

这种事情写出来就一目了然了

摩擦力

注意摩擦力的方向，它会来回变。

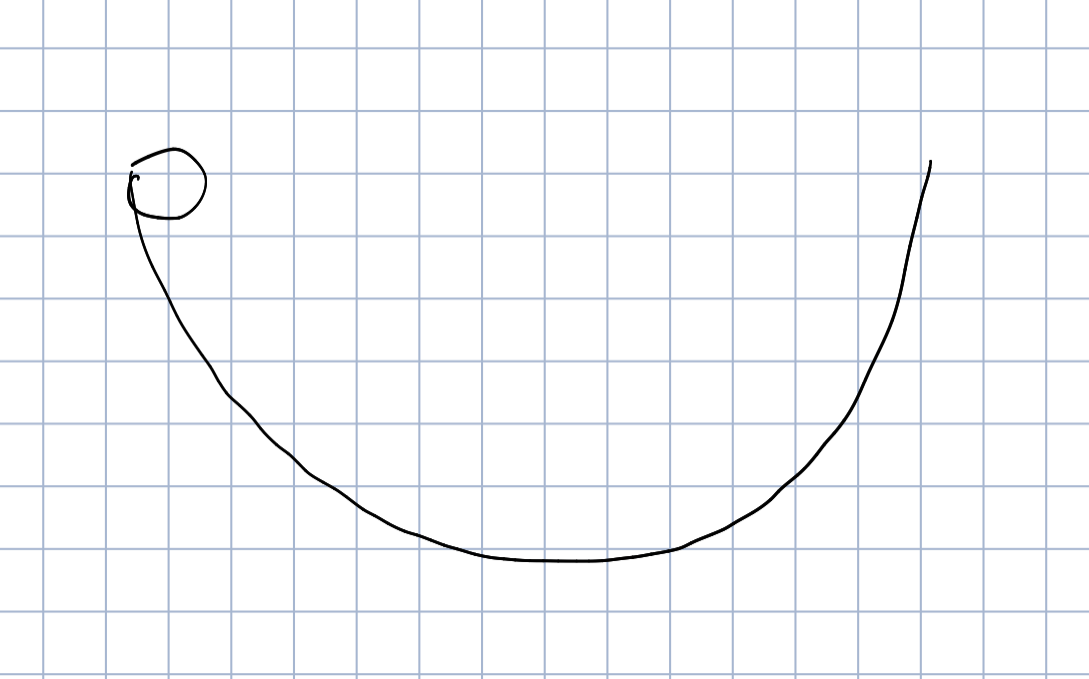
12.png

一个有摩擦的半圆弧，在左侧释放一个小球，容易知道机械能不断减小

还有就是左右侧相同高度的速度不一样，导致对圆弧压力不同

进而导致摩擦生热不同，左侧多于右边

矢量的大小

中学阶段只要说矢量的大小就是说模长，不分正负方向

所以，向上5m/s25m/s^2比向下9.8m/s29.8m/s^2小

让你求一个力，注意到，力是一个 矢量 ，所以，要把模长和方向都答出来

物理实验，越简单越好，能用天平称物体，就不要用弹簧测力计干这事

圆周运动

8.png

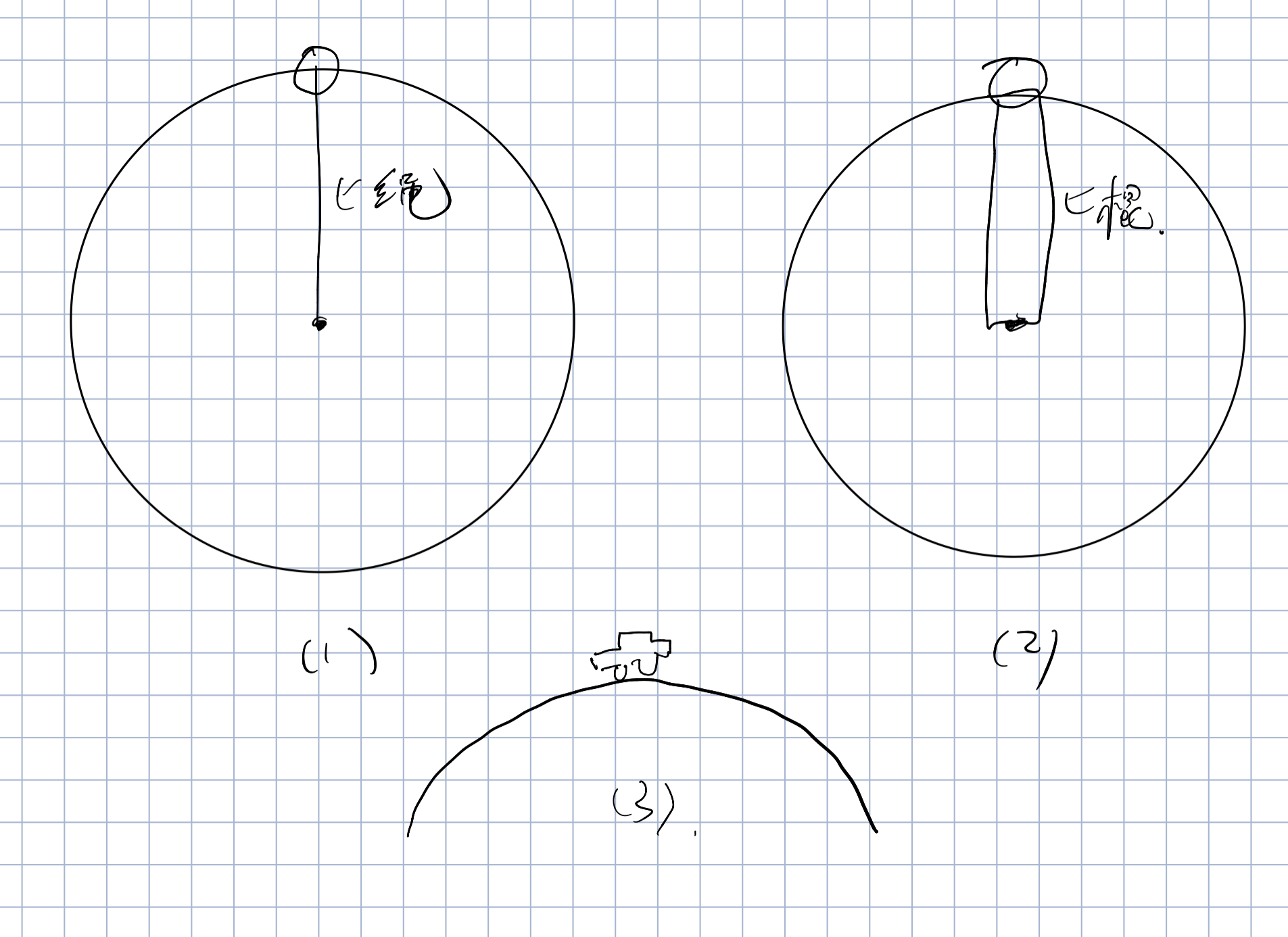
一

球绳模型，绳只能提供拉力，也就是说这个小球在最高点受到的向心力

最小就是mg，不能再小了，为了保证圆周运动，需要一个速度来抗衡它

则mg=mv2rvmin=gr\begin{array}{l} mg=m\frac{v^2}{r}\\ v_{min}=\sqrt{gr} \end{array}

二

球棍模型，既可以拉，又可以推，则最高点受向心力最小可以为0

故速度可以为零

这个模型可以推广到任何既可以拉又可以推的模型

三

小车过拱桥，这是一个只有推力没有拉力的模型，换句话说

0≤v≤gr0\le v\le \sqrt{gr}

过了就飞了

若小车以最大速度通过拱桥顶端，那么在下来时，速度一定增大

而向心力反而变成重力的分力，变小了

所以就飞出去了，也就贴不到下行的拱桥了

延伸

一个绳球模型，只要小球过了最高点，一定能做完整圆运动

卫星

同步卫星和人的角速度是一样的，可是按照高轨道低速度或者第四节天体的公式

不应该一样。这是因为人在地球上还受到了支持力，支持力和万有引力相减后才是向心力

如果有一个近地卫星，那么它一定特别特别快才是

弹簧

物体的分离

在中学阶段，认为只有当弹簧从压缩态恢复到原长时，才会与所接触物体分离

不考虑弹簧的加速度，以及速度（认为光速）

还有就是，当两个物体共速，一个物体的加速度突然比另一个小了，那么就会分离

举个例子就是，一个物体和弹簧连着，另一个没有，等弹簧恢复原长后，物块分离

劲度系数

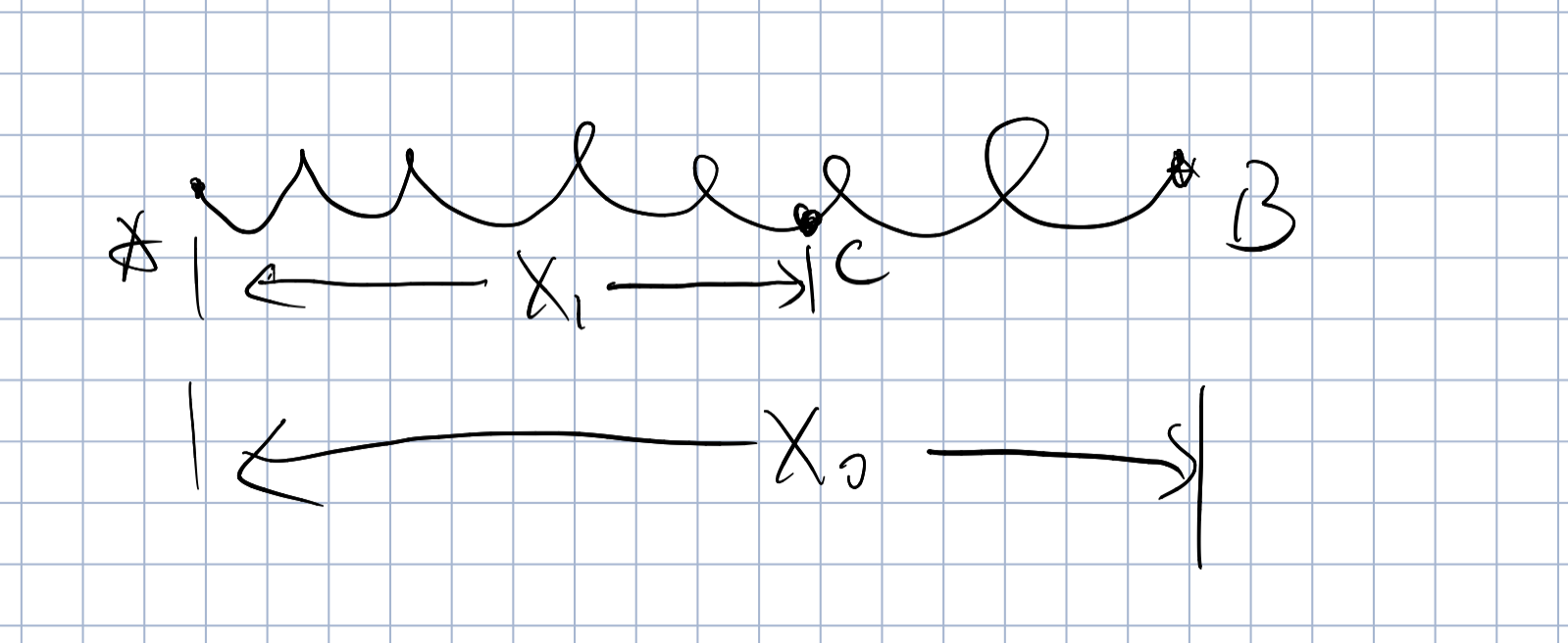
15.png

高中讨论的都是轻质弹簧，且弹力处处相等

这意味着，C点和B点弹力一样

再由弹簧的线性关系，其实B点的弹力就是T=k0(x0−x)T = k_0(x_0-x)x为原长

有CT=k1(x1−x′)T =k_1(x_1-x')x'为AC段原长

且有x0x1=xx′=x0−xx1−x′\frac{x_0}{x_1}=\frac{x}{x'}=\frac{x_0-x}{x_1-x'}

故k1k0=x0x1\frac{k_1}{k_0}=\frac{x_0}{x_1}

也即，一段弹簧中，取的越短，劲度系数越大

等效

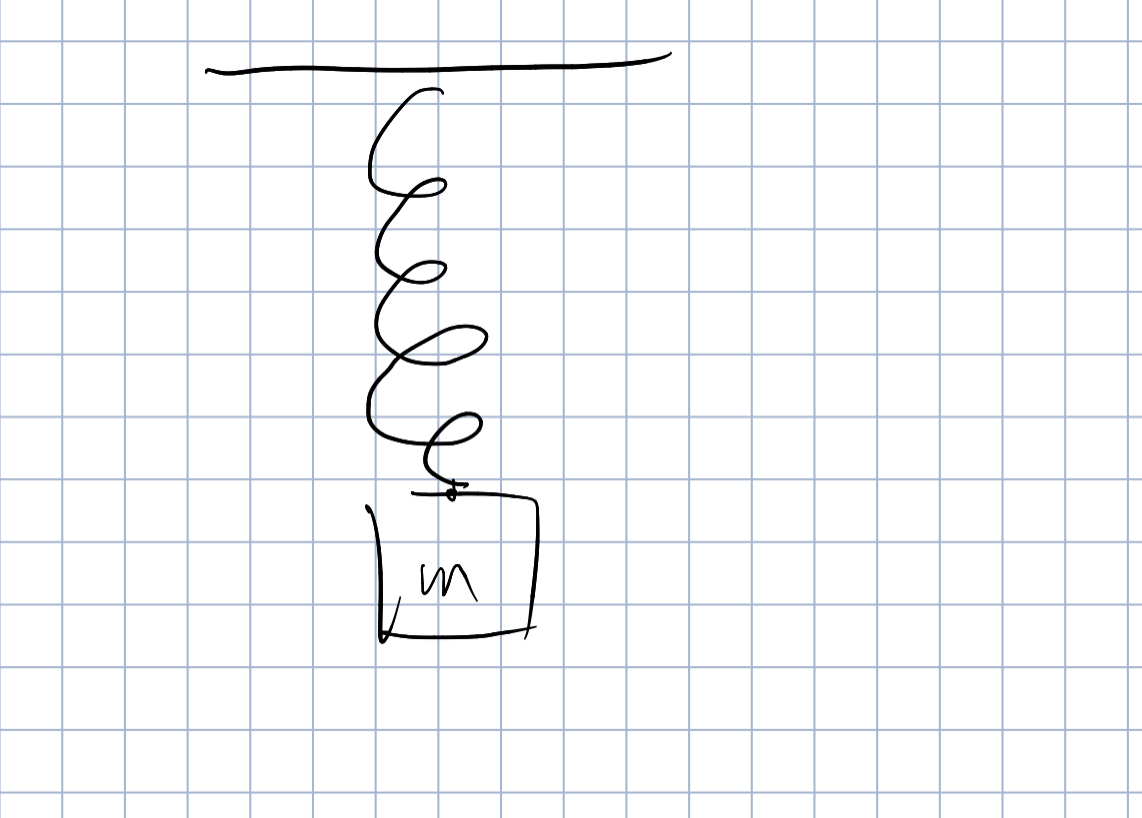
16.png

此时只需kx0=mgkx_0=mg为平衡位置就好了

这是由于弹簧的线性

弹性势能

表达式Ep=12kx2E_p = \frac{1}{2}kx^2

由弹性势能表达式可以知道很多事

比如，在x1x_1处无初速释放一个弹簧，必然能够到达原长对称的点

就是弹性势能转化为动能，再变为势能的过程而已

同理，弹簧在对称位置速度大小一定相同(无摩擦)

由于x关于时间t是正弦型函数，那么EpE_p关于时间t也是正弦型函数，且是二倍角

有的时候考试不方便用等效的手段，就可以用能量来解释

比如，借用等效的图，在原长放一个木块，问最低到多少，此时受力是什么

可以列方程mgx=12kx2mgx=\frac{1}{2}kx^2

消掉一个x再乘以2就是此时的受力2mg2mg,再除以k就是位置2mgk\frac{2mg}{k}

小技巧

9.png

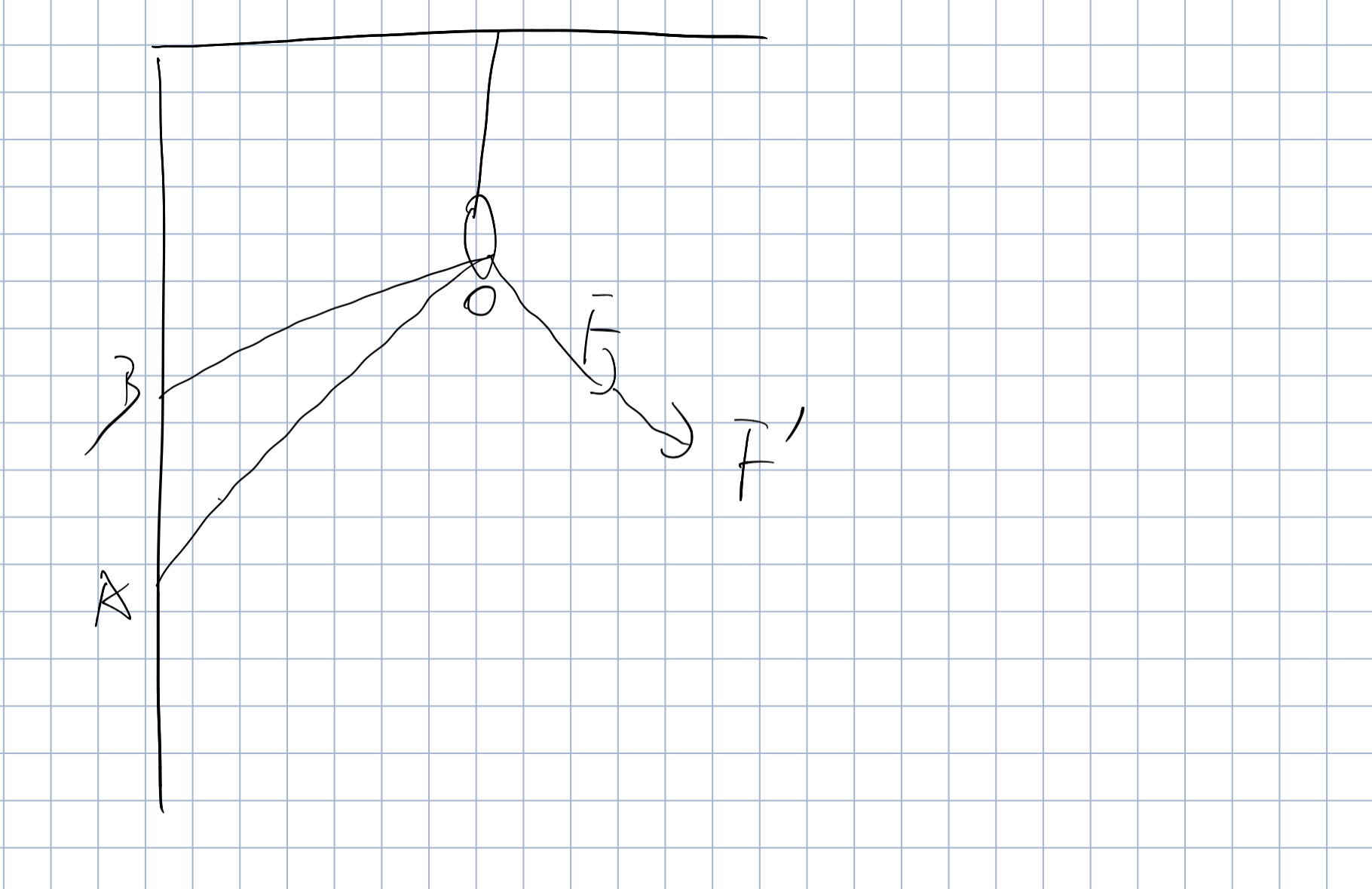
拉力做功就是F乘以绳在力的方向移动的距离

W=∣F⃗∣⋅(OA−OB)W=|\vec{F}|\cdot (OA-OB)

拓展

立体角

从平面角说起

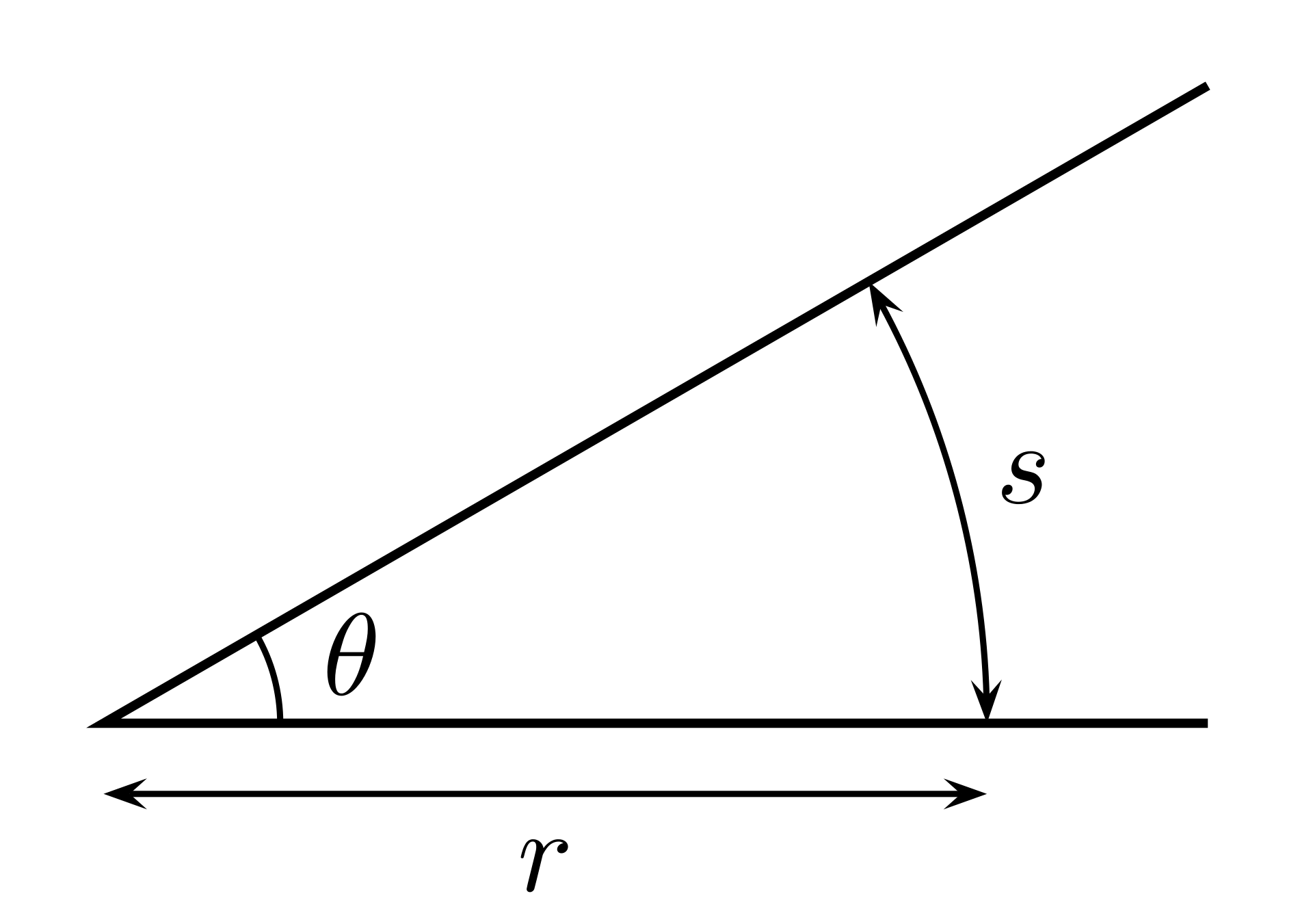
ANGLE.png

在平面上，我们可以用弧度来表示两条直线张开的程度

所以θ=sr=弧长半径\theta = \frac{s}{r} = \frac{弧长}{半径}

我们熟知，圆周角为2π2\pirad

考虑极小的角∠BAC\angle BAC（微元法）

21.jpg

由于∠BAC\angle BAC极小，所以AB⃗,AC⃗\vec{AB},\vec{AC}以及其余由A点发出，终点在它们之间的向量的方向都近似相同。

不妨取AC=AD,AE⃗\vec{AE}过CD中点，AE为单位向量，记AE⃗=r⃗\vec{AE}=\vec{r}， 位矢

CD长与弧长近似相等

想要知道∠BAC\angle BAC的弧度只需知道CDAC\frac{CD}{AC}。由于∠BAC\angle BAC极小，所以∠ADC=∠BDC=π2\angle ADC = \angle BDC= \frac{\pi}{2}。所以，CD=BCcos⁡αCD=BC\cos \alpha

又取FG⃗\vec{FG}为BC的单位法向量，可知θ=α\theta=\alpha。记l⃗\vec{l}长度为BC，方向为FG⃗\vec{FG}。最终可得∠BAC=CDAC=l⃗⋅r⃗AC\angle BAC = \frac{CD}{AC}=\frac{\vec {l}\cdot \vec{r}}{AC}

又因为此处为微元法思想，记∠BAC=dϕ,l⃗⟶dl⃗,AC=r\angle BAC = d\phi,\vec{l}\longrightarrow d\vec{l},AC=r,有dϕ=r⃗⋅dl⃗rd\phi = \frac{\vec{r}\cdot d\vec{l} }{r}

联想到三维空间

我们可以想想，三维空间有没有类似平面角的定义呢？容易从弧度想到，能不能用一个球相关的东西表示呢？没问题！立体角=球面积(半径)2立体角=\frac{球面积}{(半径)^2}

直观上来看就是一个类似锥形的东西，那就是立体角了

23.jpg

至于说为什么是平方。是因为球的表面积公式是4πr24\pi r^2。这样一除，不就容易消掉东西了嘛

记立体角为Ω\Omega,有Ω=sr2\Omega = \frac{s}{r^2}

单位是sr(球面度)，类比rad(弧度)

所以一个球的球面角就很好求了，是4π4\pi。

面向量

想不到吧，面也可以是向量，我们记一个平面的向量s⃗\vec{s}。模长就是这个平面的面积，方向是这个平面法向量的方向

立体角的求法

有了面向量，类比弧度的微元表达式，我们有dΩ=r⃗⋅ds⃗r2d\Omega=\frac{\vec{r}\cdot d\vec{s}}{r^2}

注意分清位矢(r⃗\vec{r})和半径(r)

均匀球壳内部的场强

22.jpg

里面那个红色的，是一个密度均匀的球壳，任取一点P，球壳对它产生的场强在三个方向进行分解。由于球体完美的对称性，PH，PI方向不可能有场强，只需转动一下便知

所以只在PE方向可能有场强。你可能注意到，PE方向，正是原点到P的位矢的方向

并且以O为圆心，OP为半径的球上，任意一点的场强大小都相等

通量

定义通量dΦ=E⃗⋅ds⃗d\Phi=\vec{E}\cdot d\vec{s}

E为场强，s为场强通过的一个曲面

由于只在PE方向有场强，所以在以O为圆心，OP为半径的球上，任取一小块面积，它们的通量都是Es，因为场强的方向恰好和面向量的方向一致

所以总的通量就是这个面上任一点的场强乘以球面的表面积，写下来是Φ=4πr2E\Phi = 4\pi r^2E

接下来我们只需要证明在均匀球壳得到内部的任意一个面的通量是0，就可以证明内部场强是0，进而说明均匀球壳对内部物体合力为0了

以点电荷为例

电场力和万有引力都遵循平方反比的规律

电场强度E⃗=kqr⃗r2\vec{E}=\frac{kq\vec{r}}{r^2}

r⃗\vec{r}是场强的方向上的单位向量，也就是，从点电荷出发，指向你想要算场强的那个位置的向量，或者叫位矢

所以通量就是dΦ=E⃗⋅ds⃗=kqr⃗r2⋅ds⃗=kqdΩd\Phi=\vec{E}\cdot d\vec{s}=\frac{kq\vec{r}}{r^2}\cdot d\vec{s}=kqd\Omega

dΩd\Omega是立体角

所以总的通量就是Φ=kqΩ\Phi=kq\Omega

这表示，一个曲面的全部电通量和它关于点电荷张成的立体角有关

如果点电荷在曲面内，那么张成的立体角就是4π4\pi

那如果点电荷在曲面外呢？我们回归二维来看看

24.jpg

要算闭合曲线关于点A所成的角度。一种理解是，先选一个点，沿着曲线走到尽头，看看最后弧度是多少，结果闭合曲线你找不到头或者说走一圈回来了，所以所张开的弧度是0.

另一种理解是把每一小段的平面角加起来，最后得到最终答案。我们说过，直线是有法向量的，一段闭合曲线的任意一小段也有法向量，且BC段法向量的方向与DE段法向量的方向应该不同，都是朝着曲线外的。再根据平面角的微元表示，可以知道BC的法向量与位矢成钝角，DE则成锐角，二者形成的平面角正好大小相等，符号相反，两者抵消了，所以张开的弧度为0

推广到三维空间，一个闭合曲面对曲面外点电荷张开的立体角为0

所以Φ=4πr2E=0\Phi=4\pi r^2 E =0

场强为0

所以在均匀球壳中，任做球面，上面任意一点所受场强为0，即球壳对内部任意一点合力为0（该结论只对均匀球壳成立）

  1. 错题
    1. 单摆
    2. 动量守恒定律
  2. 小结论
    1. 第一种情况
    2. 第二种情况
    3. 第三，四种情况
    4. 消去
      1. 圆锥摆
      2. 摩擦力做功
    5. 题目中的流体力学
      1. 白努力方程的简单推导
      2. 定常流
      3. 流体的重力势能
        1. 回顾
  3. 简单电路
    1. 限流电路
    2. 分压电路
  4. 天体
  5. 能量
    1. 对于任意势能
    2. 能量守恒的本质
      1. 推广
      2. 结论
    3. 重力势能
    4. 能量损失
    5. 做功的定义
    6. 内能
  6. 力学
    1. 平抛
      1. 结论
    2. 绳子
  7. 矢量的分解
  8. 易错点
    1. 摩擦力
    2. 矢量的大小
  9. 圆周运动
    1. 一
    2. 二
    3. 三
      1. 延伸
    4. 卫星
  10. 弹簧
    1. 物体的分离
    2. 劲度系数
    3. 等效
    4. 弹性势能
  11. 小技巧
  12. 拓展
    1. 立体角
      1. 从平面角说起
      2. 联想到三维空间
      3. 面向量
      4. 立体角的求法
    2. 均匀球壳内部的场强
      1. 通量
      2. 以点电荷为例
≡