对于函数y=f(x)
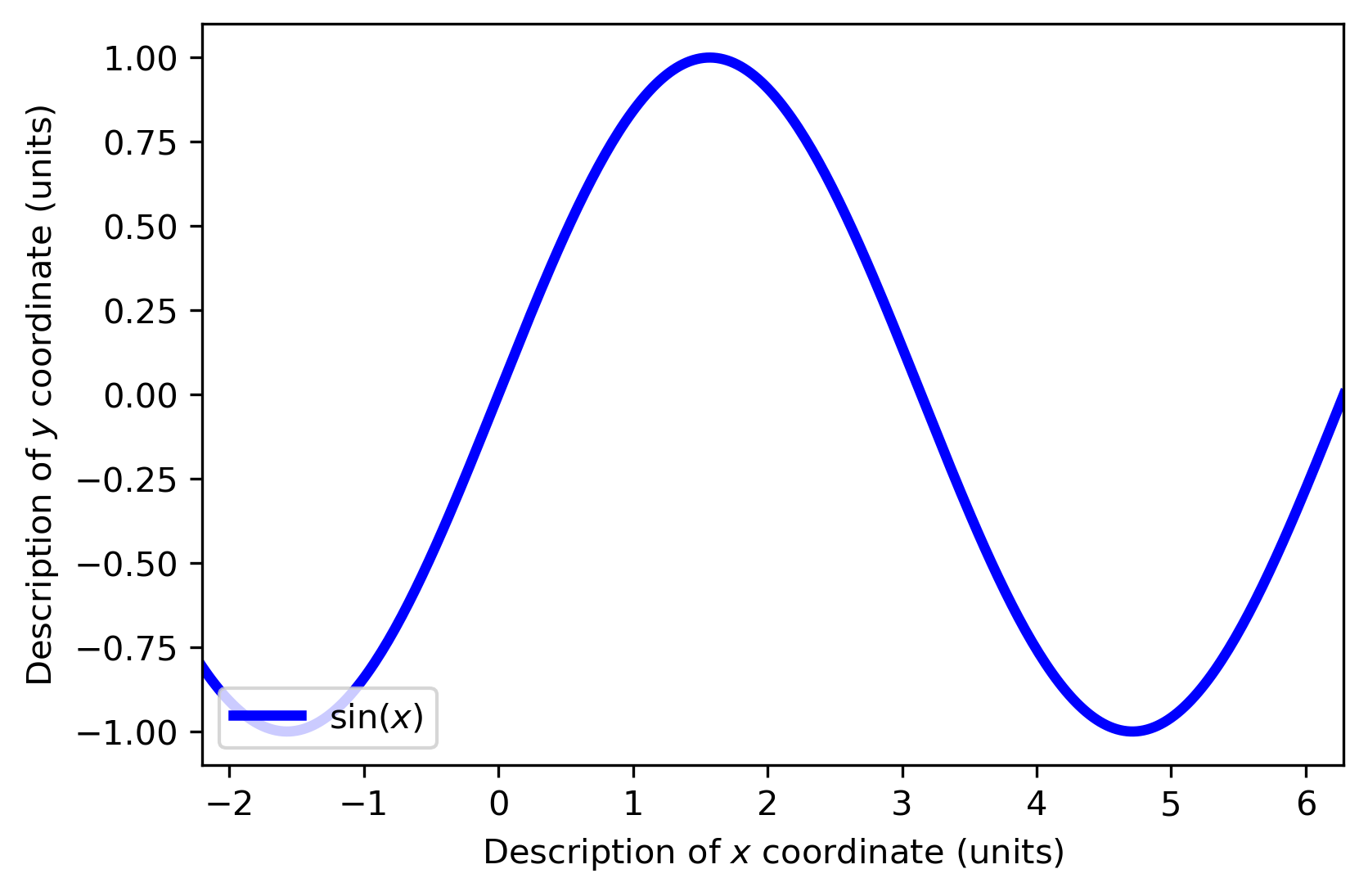
其上任意一点(x0,f(x0))y0=f(x0)
首先对其做平移变换,将函数向左平移2π个单位得到(x0−2π,f(x0))
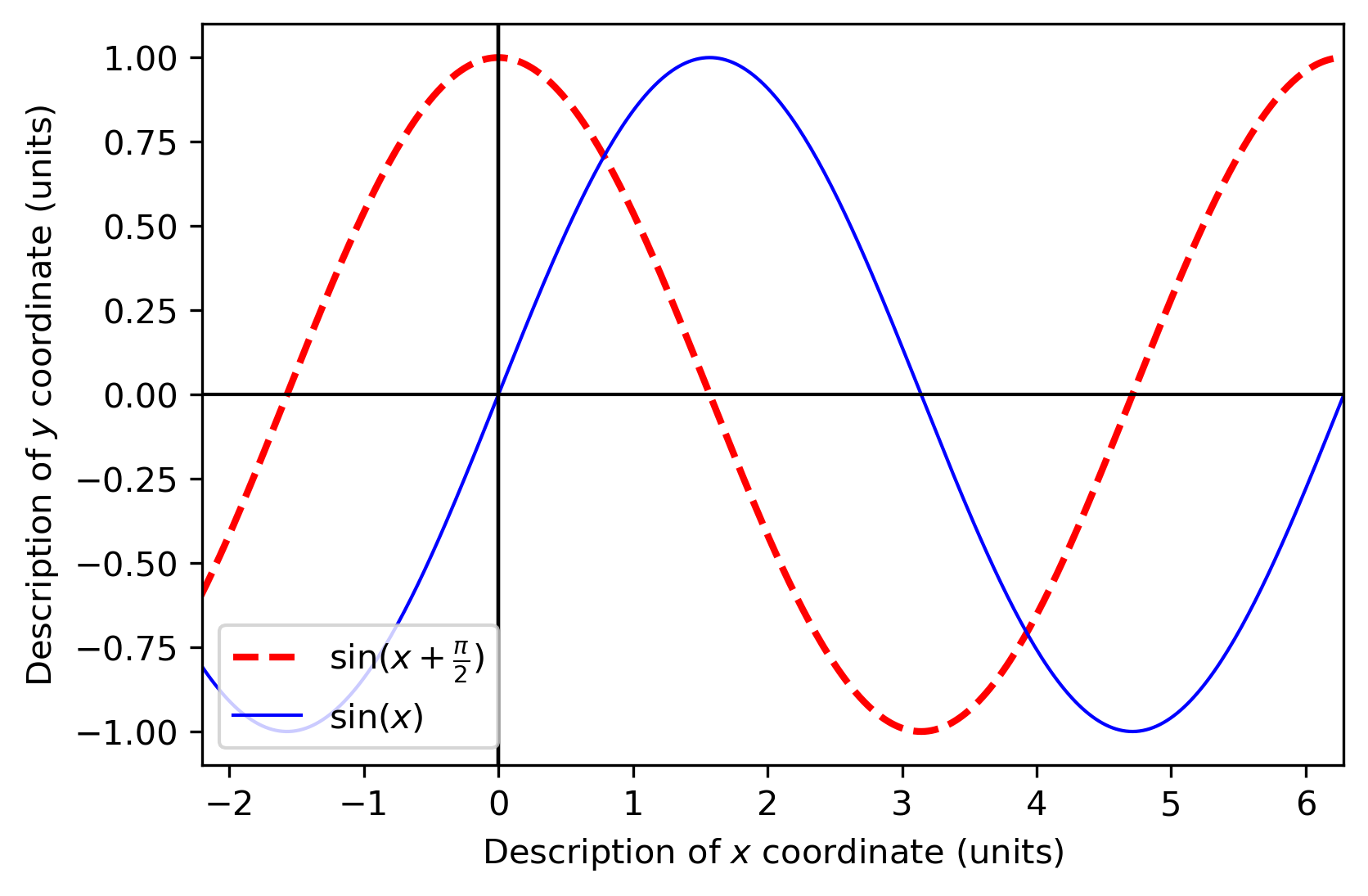
再对其进行伸缩变换,使此刻所有横坐标变为原来的2倍得到(2(x0−2π),f(x0))
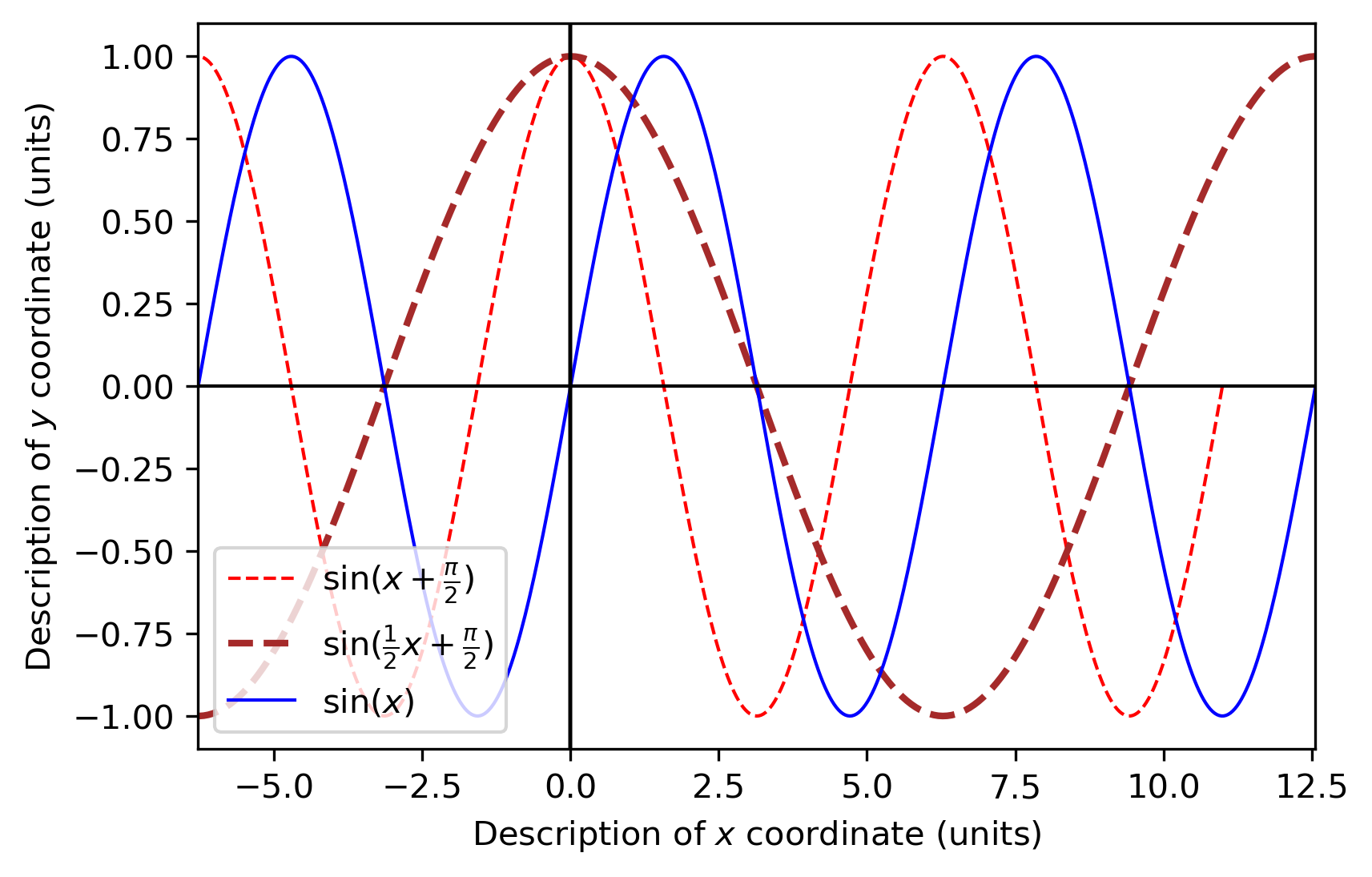
再在竖直方向进行拉伸两倍得到(2(x0−2π),2f(x0))
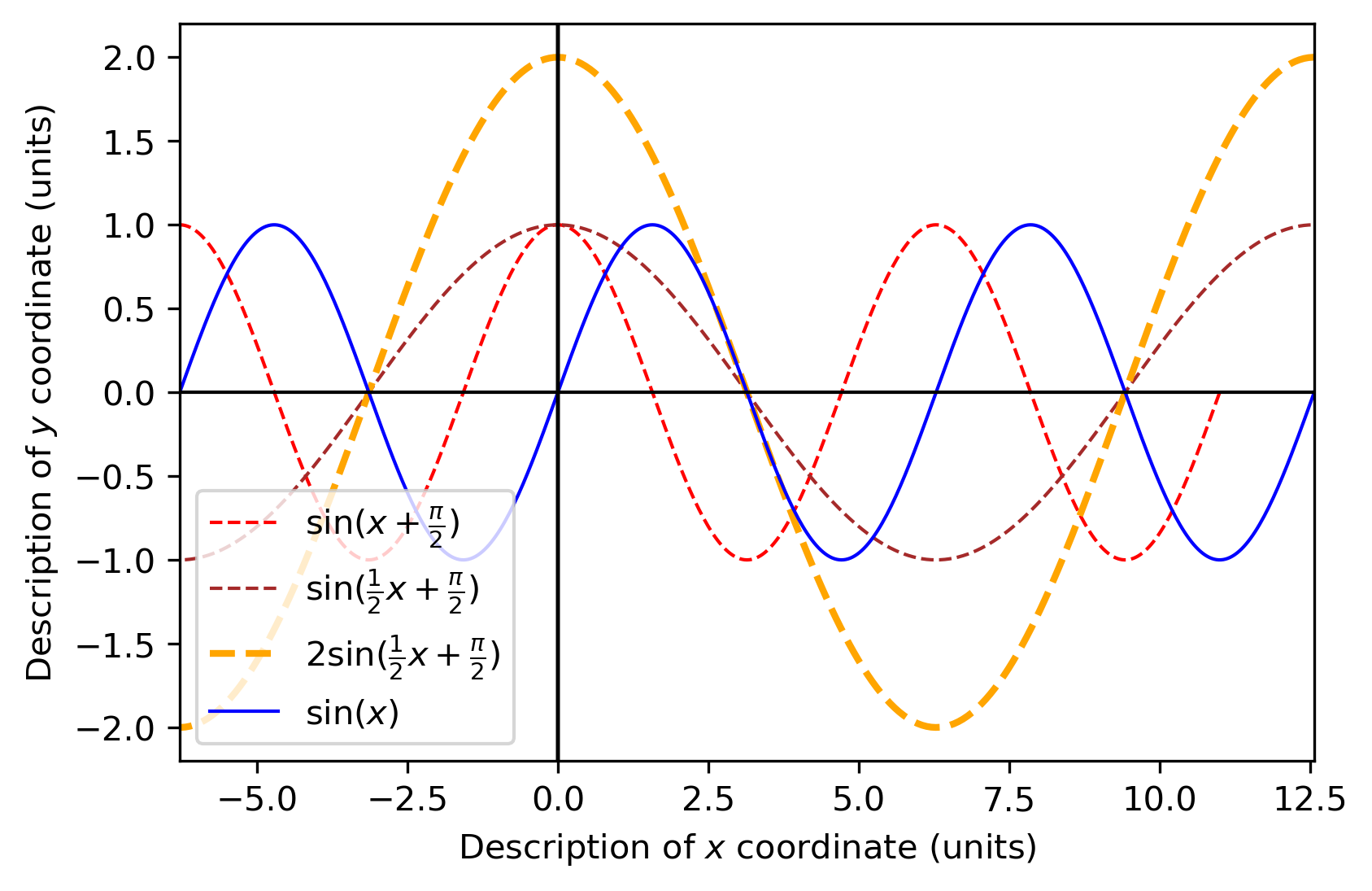
最后得到关系式x′=2x0−πy′=2y0
其中y0=f(x0)
变换可得x0=21x′+2πy0=21y′
带入可得21y′=f(21x′+2π)
容易知道对于任意的(x′,y′)y=2f(21x+2π)
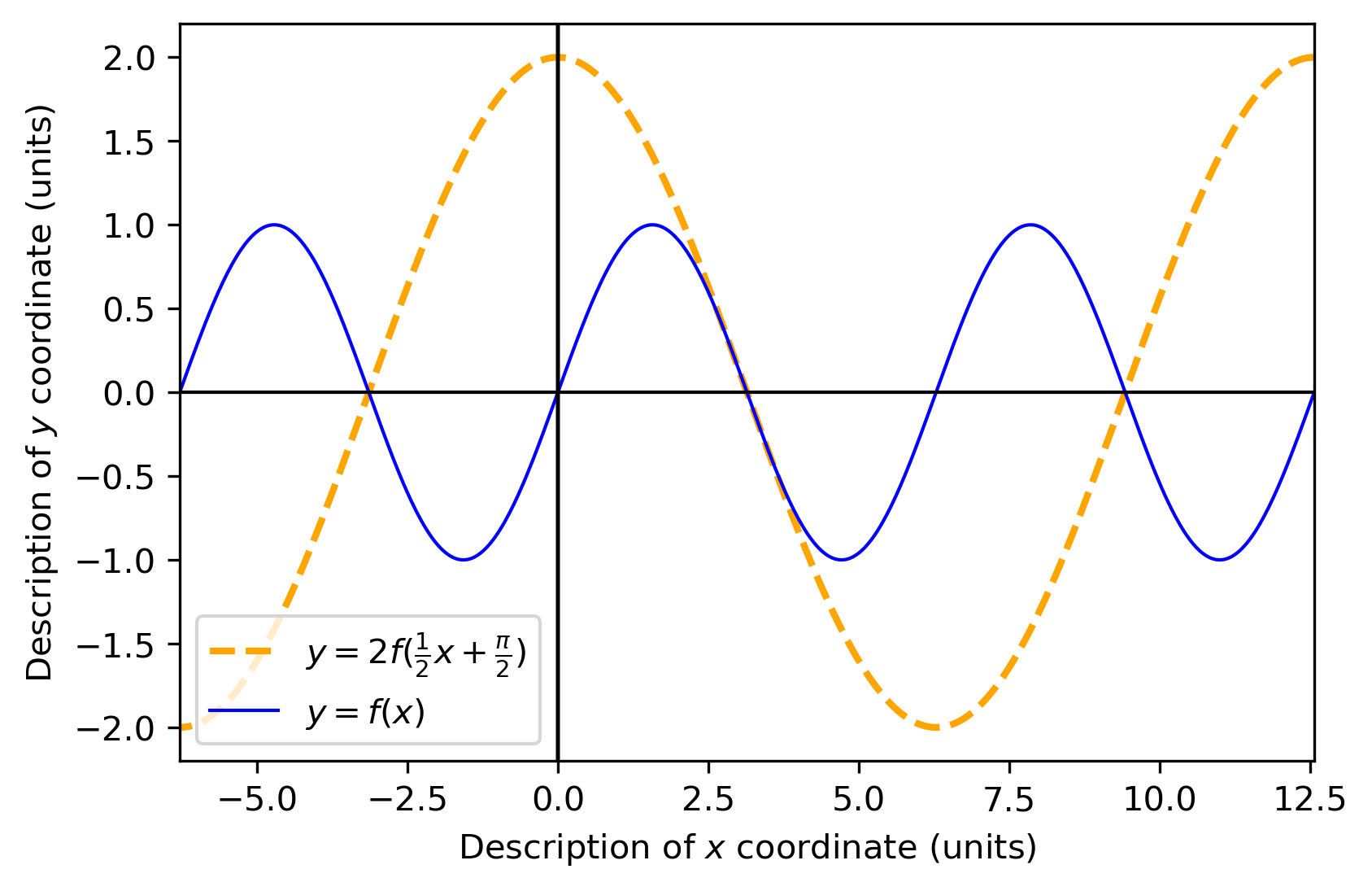
同理,对于y=f(x)
先把横坐标拉伸2倍(2x0,y0)
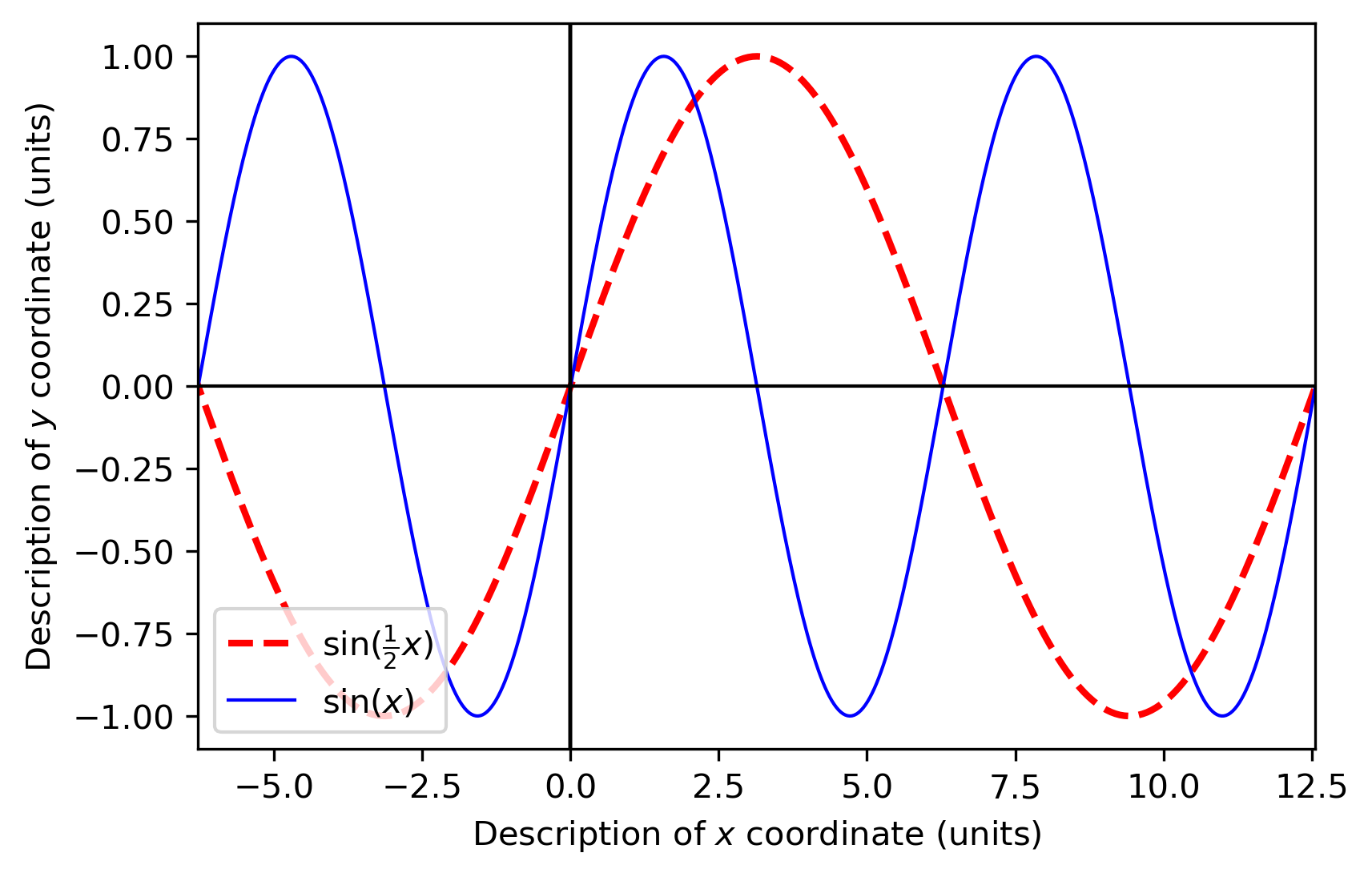
再右移3个单位(2x0+3,y0)
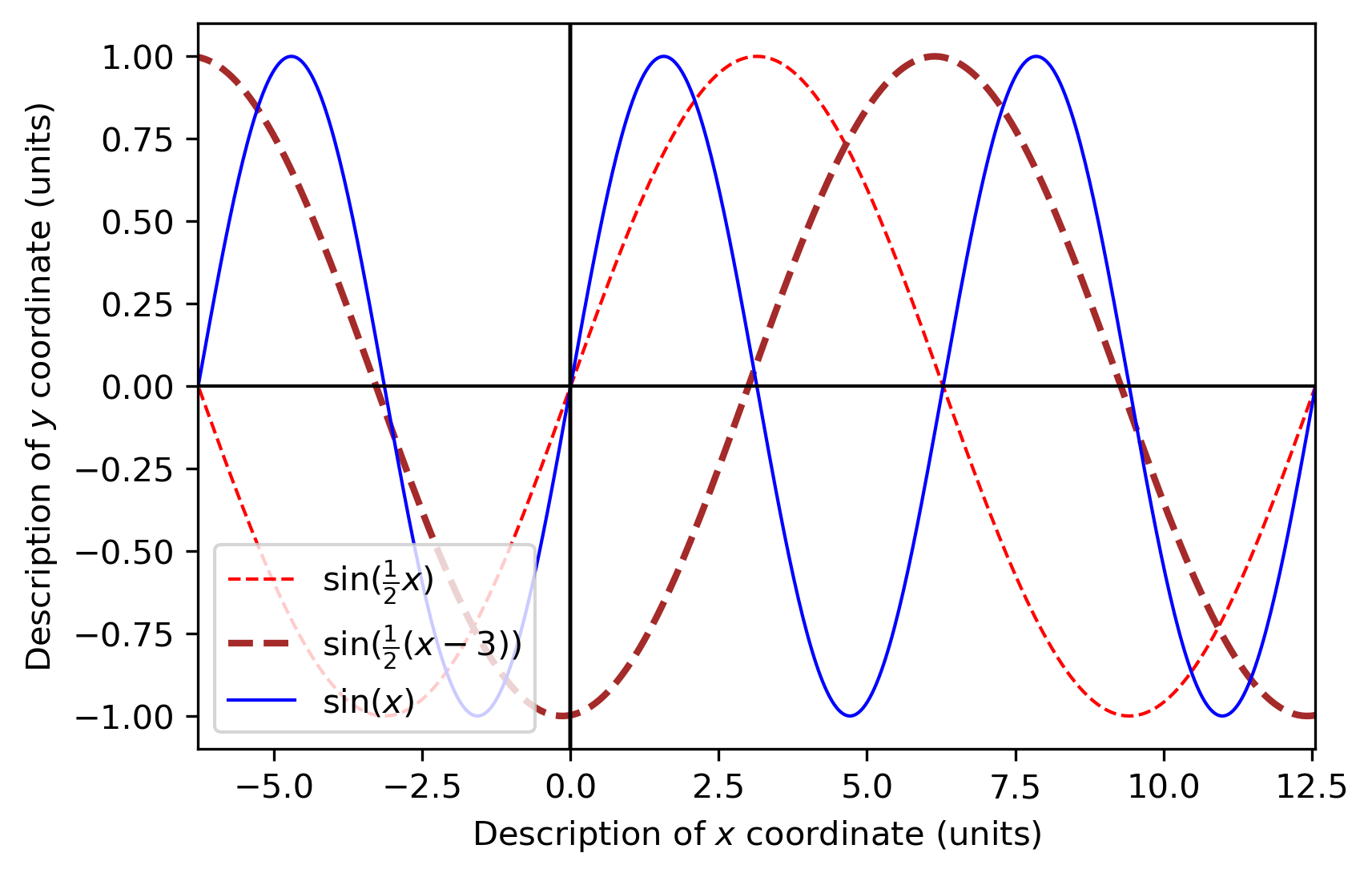
再竖着拉伸31倍(2x0+3,31y0)
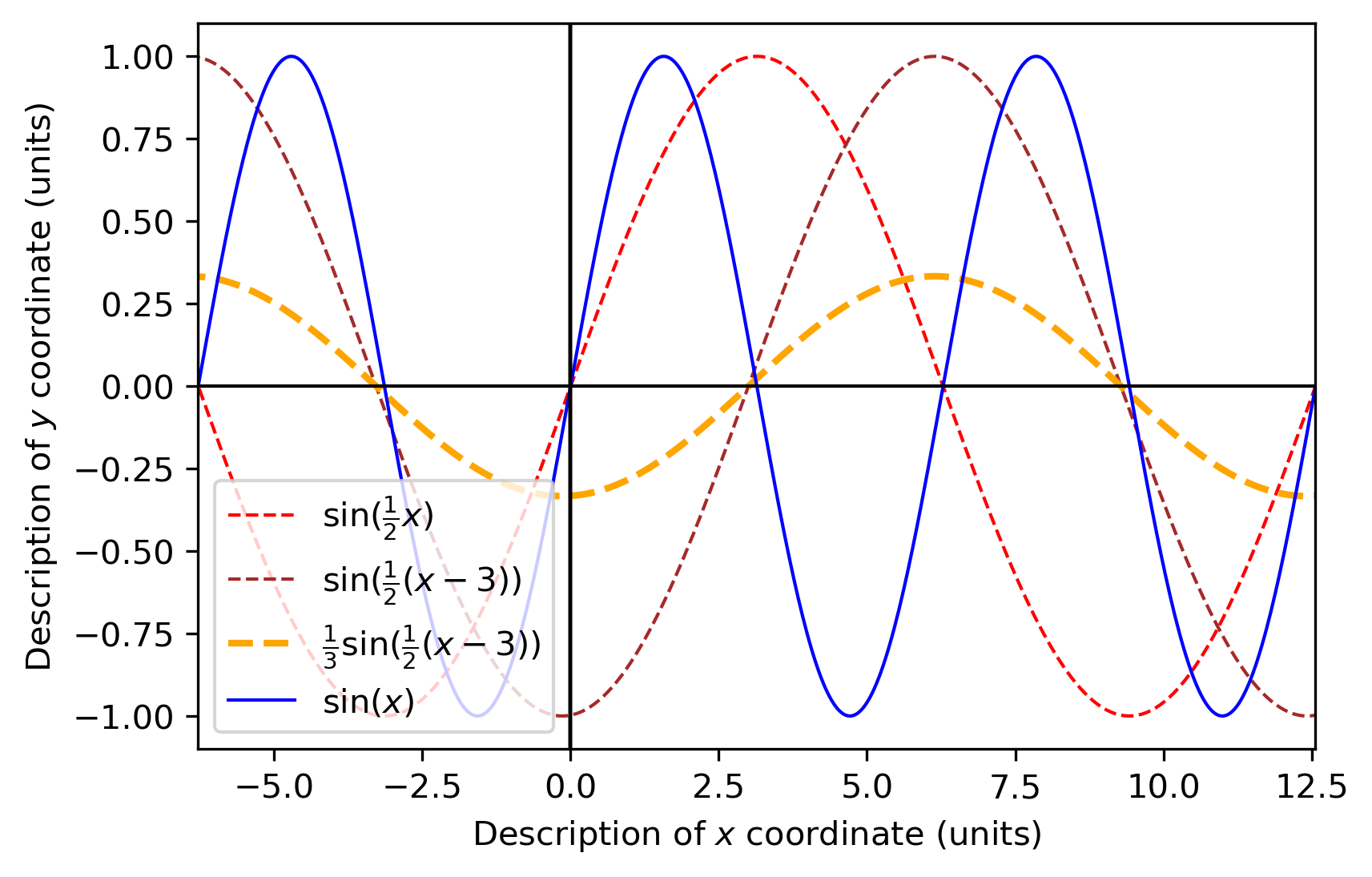
有对应关系x′=2x0+3y′=31y0
代入有y′=31f(21(x′−3))
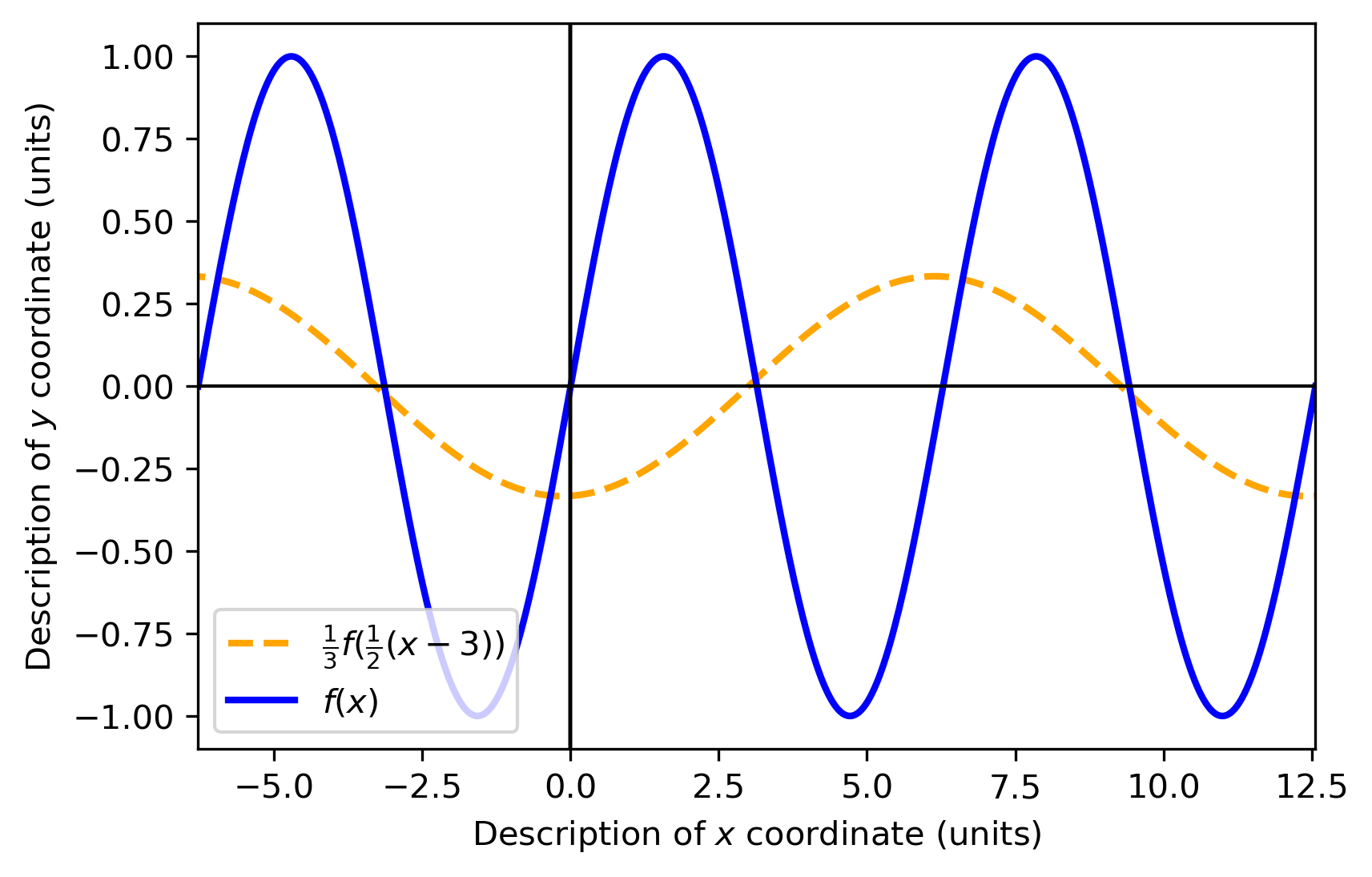
把y=f(ωx+ϕ)向左平移m个单位
对于点(x0,y0)有映射f:ωx0+ϕ⟶y0
平移后的点为(x0−m,y0)
记x0−m=x1则有映射f:ω(x1+m)+ϕ⟶y0
即对于变换后的点而言任意给出的x与y有关系式y=f(ω(x+m)+ϕ)
直接有推论y=f(ωx+ϕ)=f(ω(x+ωϕ))可以由y=f(ωx)向左平移ωϕ个单位得到
同理,把y=f(ωx+ϕ)在水平方向拉伸k倍
拉伸后的点为(kx0,y0)
记x2=kx0有f:ωkx2+ϕ⟶y0
平移后的函数即为y=f(ωkx2+ϕ)
在水平方向的伸缩不改变ϕ
水平方向的平移作用在ω的括号里
如何快速y=f(ω1x+ϕ1)⟶y=f(ω2x+ϕ2)
根据推论首先改ω不改变ϕ
即在水平方向伸缩ω2ω1倍得到ω1x0=ω2x1x1=ω2ω1x0
然后再水平平移,我不写了,你懂得
锐角三角形ABC中,欲证sinA+sinB+sinC>cosA+cosB+cosC
注意到A+B>2π
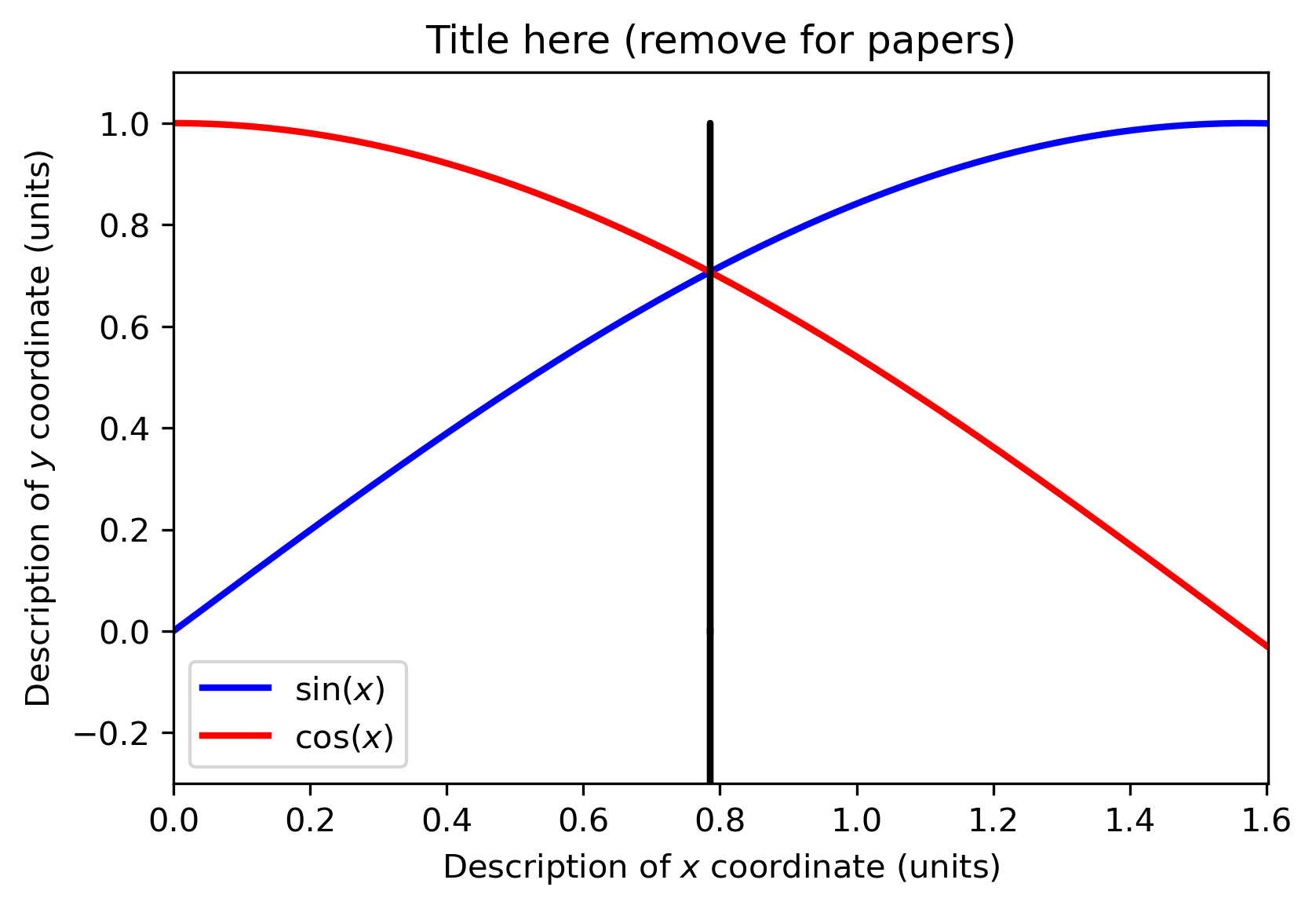
注意到4π−A<B−4π
所以有sinA>cosB得证
比如斜率为0啊,二次函数首项系数为0啊啥的,这一写,不就有分了?先写上再说
导数切线题注意看好,是 在 某点的切线,还是 过 某点的切线
概率题,把事件写上,要不然扣分!
⎣⎢⎢⎢⎢⎡a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn⎦⎥⎥⎥⎥⎤
条件告诉你aik=ajk说的是啥意思呢
说的是同一列中的第i个和第j个不等!
注意到向量的角度从0取到π,其中,0不是锐角,π不是钝角
简单回顾
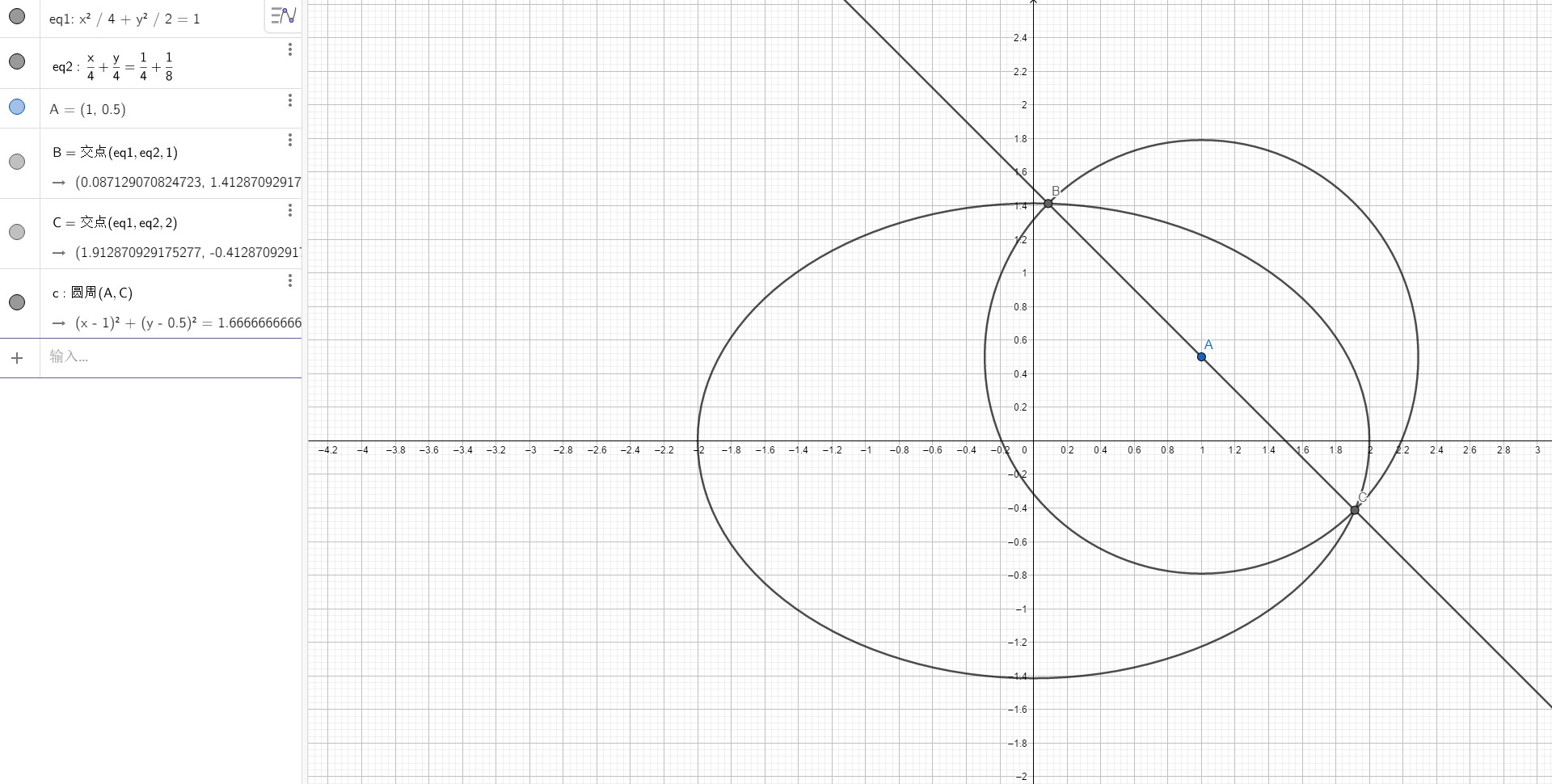
对于任意二次曲线A1x2+B1y2+C1xy+D1x+E1y+F1=0A2x2+B2y2+C2xy+D2x+E2y+F2=0
过它们交点的二次曲线可以写成μ(A1x2+B1y2+C1xy+D1x+E1y+F1)+λ(A2x2+B2y2+C2xy+D2x+E2y+F2)=0
这时候,只要配配系数就可以解决问题了
比如圆的方程必没有xy项,且x2和y2系数相等
椭圆Ax2+By2+F=0
椭圆外一点E在定直线x=C上运动,与左顶点A与右顶点B连直线交椭圆于四个点ACBD
证明AB与CD交点为定点
只需设出lEA和lEB的方程并乘在一块再与椭圆方程构建二次曲线系
就可以得到一定过ABCD四个点的二次曲线
随后,把lAB和lCD的直线根据CD过定点设出来,调参数即可
中点弦是指,这有一个点,过这个点的直线与二次曲线恰好交于两点,这个点是中点,那么这条直线就能确定了
对于任意二次曲线Ax2+By2+Cxy+Dx+Ey+F=0
设(x0,y0)为那个中点
则有另外两个被分成两段的点(x1,y1),(2x0−x1,2y0−y1)
立刻有方程Ax12+By12+Cx1y1+Dx1+Ey1+F=0(1)A(2x0−x1)2+B(2y0−y1)2+C(2x0−x1)(2y0−y1)+D(2x0−x1)+E(2y0−y1)+F=0(2)
(2)-(1)得到A(4x02−4x0x1)+B(4y02−4y0y1)+C(4x0y0−2(x0y1+y0x1))+D(2x0−2x1)+E(2y0−2y1)=0
化简得到(2Ax0+Cy0+D)(x1−x0)+(2By0+Cx0+E)(y1−y0)=0
看得到(2Ax0+Cy0+D,2By0+Cx0+E)是该直线的法向量
所以中点弦即为(2Ax0+Cy0+D)(x−x0)+(2By0+Cx0+E)(y−y0)=0
或者这个形式(2Ax0+Cy0+D)x+(2By0+Cx0+E)y=(2Ax0+Cy0+D)x0+(2By0+Cx0+E)y0
注意到(x0,y0)关于该曲线的极线为Ax0x+By0y+C2x0y+y0x+D2x0+x+E2y0+y+F=0
或者换一种写法(2Ax0+Cy0+D)x+(2By0+Cx0+E)y=−2F形式相近,方便记忆
求中点弦只要把这个点的极线写出来,左边只放x和y,在右边放x和y对应前面的系数和x0,y0
举例,椭圆Ax2+By2+F=0的中点弦是Ax0x+By0y=Ax02+By02
简单的定义∀a∈A,∃b=a∈B⇒A⊆B
简单的应用if∀x1∈D1,f(x1)∈A,∃x2∈D2,g(x2)∈B⇒A⊆B
其中,A和B分别为x∈D1时f(x1)的值域和x∈D2时g(x2)的值域
见到形如xy+x1+y1=1的式子该怎么处理呢?
①可以两边乘以xy然后当作x的二次函数来解
②可以利用(a+1)(b+1)=ab+a+b+1这个结论
③换元⎩⎪⎨⎪⎧xy=ax1=by1=c
有{a+b+c=1abc=1
椭圆小题,只告诉焦点和切线可以想
- 光学性质
- ∣F1P∣∣F2P∣=b2(辅助圆)
推论是可以通过辅助圆和切线比较准确的找焦点
对于偶数来说,可以表示为2n以及2m⋅c其中c=2k+1k∈N+
对于(i+j)(i−j)(i,j∈N+)
可以表示除了1,2之外的所有自然数
而对于(i+j)(i−j+1)(i,j∈N+)
来说,可以表示除了2的幂之外的所有偶数
给定一个不是2的幂的偶数,必然能写成2m⋅cwherec=2k+1k∈N+
则只需令i+j=2mi−j+1=c=2k+1
就能解出一组(i,j)
对于任意一道导数题,先观察一下函数是否过某定点,与参数无关的,可以尝试验证±1,±2,±e,很可能后面要用到。该技巧适用于一切函数题。
算两条曲线的交点时需要注意,除了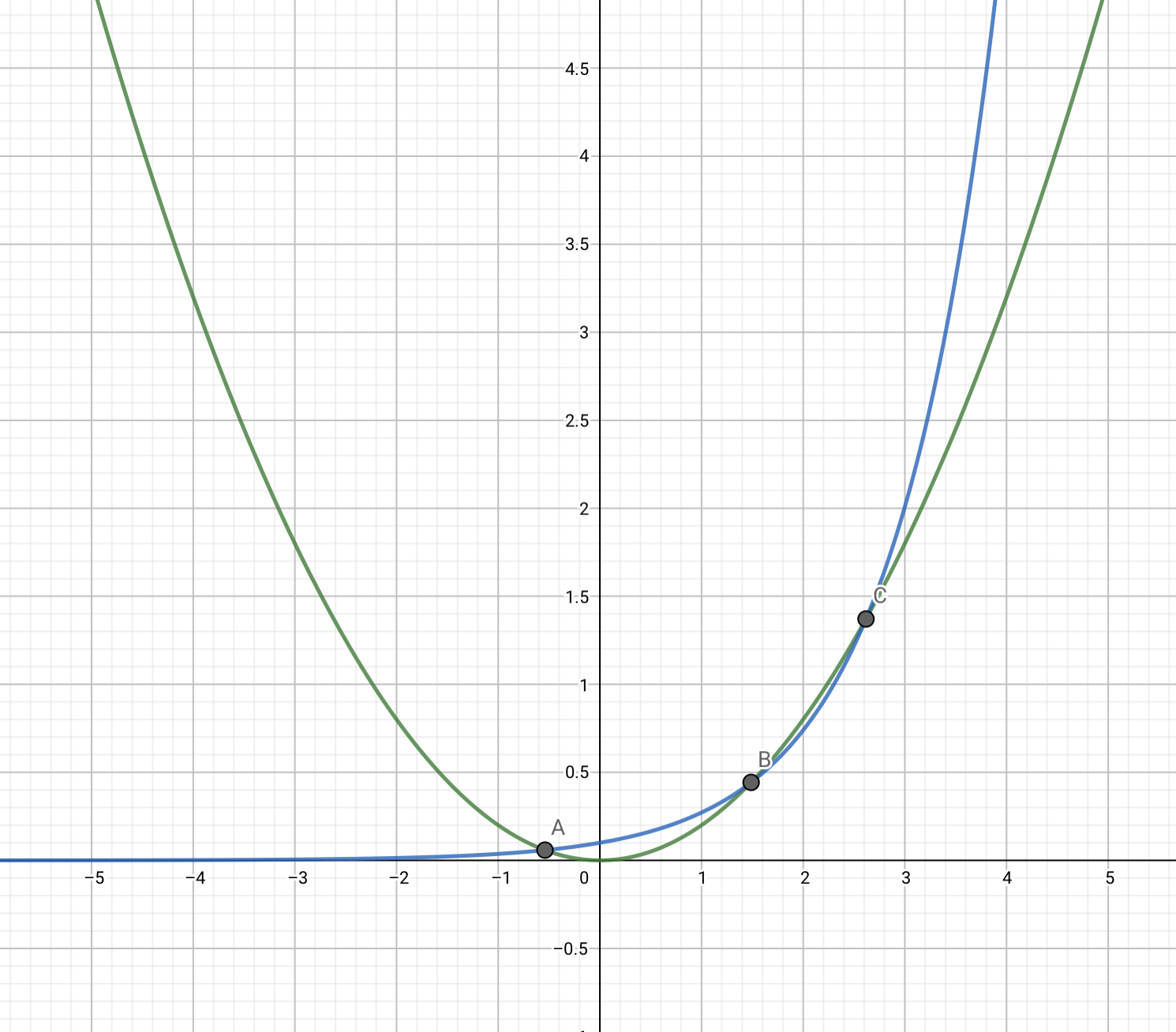
还有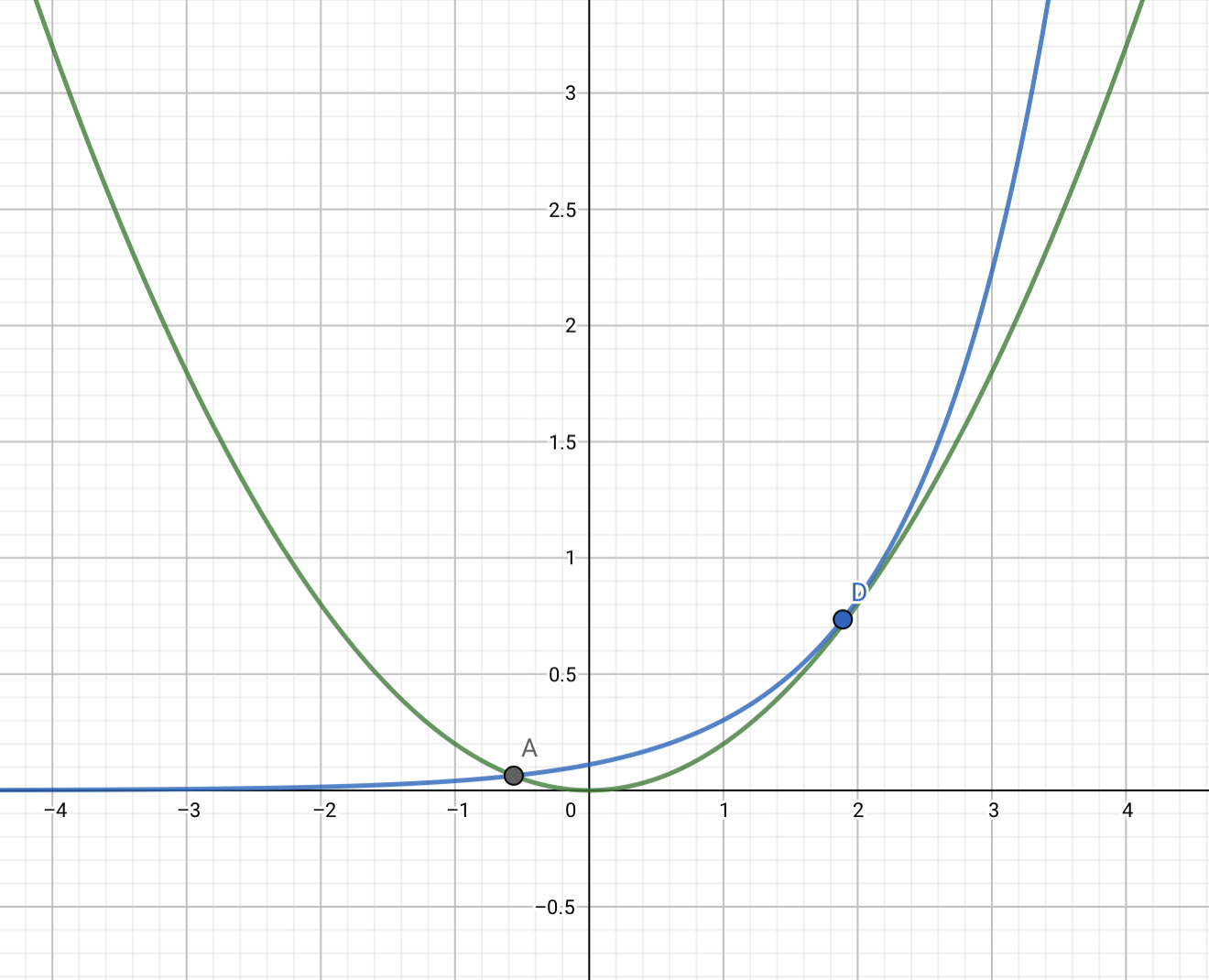
不过其实我们发现算两条曲线是麻烦的,我们最好转化成一条直线和一条曲线
对于n(n+1)(n+2)(n+3)(n+4)这样的整式,可以n(n+1)(n+2)(n+3)(n+4)=61[n(n+1)(n+2)(n+3)(n+4)(n+5)−(n−1)n(n+1)(n+2)(n+3)(n+4)]
-
要抽象思考,比如说,你要求的东西只跟集合的基数有关(cardinality),那就没必要关注具体的细节,直接计算card就行
-
注意 奇偶分析 会是极其有用的手段。有的时候可以直接用奇数和偶数来代替你要写的具体的项(mod2),举个例子∣an+1−an∣=1,且a1=0,你发现,写出每一项是不好写的,但是写奇偶是没问题的,奇数项为1,偶数项为0,这样的手段往往可以帮你快速判断或证明一个命题为假
-
有时候一定要想想,我正在求的东西我真的在乎吗?我真的在乎里面具体每一个数吗?我大概是不在乎的,抽象点!
-
一个n元集合A={a1.....an}的所有子集可以用一个n位的2进制数表示,或者,n维向量进行表示,用1和0来代表选或没选该元素,好处是 可以用0来湮灭我所不需要的东西 。比如我告诉你A的不同的两个子集的交集的card是个偶数,就可以变成,Bi⋅Bj=2nn∈N+,这样我就又可以通过点乘来奇偶分析了!
-
见到新定义的运算,立马去想基本运算律,比如0元,逆元,单位元。结合律,交换律,分配律
-
当你发现要处理有关无理数的数论问题时,基本上就是思路错了,仔细揣摩条件,寻找矛盾,比如条件给你一个公比大于2的等比数列,你就证它公比大于2是有问题的。












